 deutsche Version
deutsche Version| Manfred Börgens Mathematics on stamps |
stamp list previous stamp |
main page |
 deutsche Version deutsche Version |

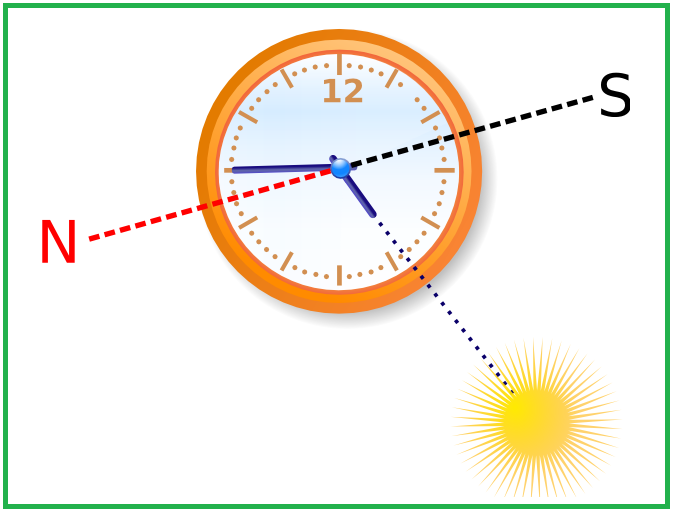
Figure 1 Finding South with a watch and the position of the sun Copyright
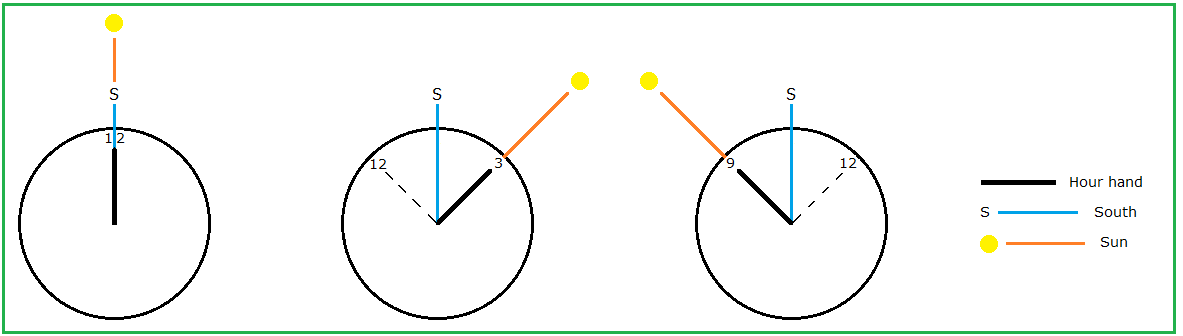
| Computation of the angle in the scouts' method
τ time measured in degrees: τ = 0° = 00:00 , τ = 90° = 06:00 etc. (True Sun Time) This is not the angle shown by the watch but half of it! τo time shown on the watch: τo = τ/15° A Azimuth (angle of the sun read along the horizon): A = 0° = North, A = 90° = East etc. The middle and the right graphics in figure 2 show the increase of the angle between the North direction as assumed by the scout and the azimuth; it amounts to 15° per hour. (E.g., if in the right graphic in figure 2 we would take 10:00 instead of 09:00 the angle between the hour hand and the 12 on the watch would grow by 30° , thus the angle between the hour hand and the assumed South direction would grow by 15°.) This yields a very simple formula for the scout when she or he assesses the direction of the sun: (1) AScout = τo·15° = τ |
| Computation of the angle for the true position of the sun
The true azimuth depends on three parameters: time of day, date and latitude. (The scouts' method only uses time.) The date is usually replaced by the declination of the sun. This is the latitude where at noon the sun stands in the zenith. The translation from date to declination and back is made with a declination table. τ time measured in degrees: τ = 0° = 00:00 , τ = 90° = 06:00 etc. (True Sun Time) δ declination φ observer's latitude Pertinent sources give different (but equivalent) formulae for the azimuth. These make simplifying assumptions (spherical shape of the earth, no atmospheric refraction) which in our context generate merely small and negligible deviations. We take the formulae deduced in Blog # 3, formula (14) on this website. Due to the symmetry a.m./p.m. explained above it is sufficient to compute A for the time before noon: (2) Atrue = arccot(cot τ sin φ + csc τ tan δ cos φ) Remark: The Mathematica definition of arccot is the inverse function of cot:[-π/2,π/2]\{0} → R , in contrast to the more familiar definition as the inverse function of cot:(0,π) → R , which we used in Blog # 3. If you want to compute A with Mathematica you should use the Mathematica function acot[x_]:= ArcCot[x] + If[x<0,π,0] instead of ArcCot[x] . Furthermore, for Atrue as well as for AScout we get: τ = 0° ⇔ A = 0° and τ = 180° ⇔ A = 180°. At day time τ , we derive from (1) and (2) the difference between the South direction and the azimuth : SouthScout = 180° - τ = 180° - AScout Southtrue = 180° - Atrue (3) Southtrue - SouthScout = AScout - Atrue We shall see that this difference between true and assumed South direction can be considerable. |
| Sunrise
For the scouts' method being employed the sun must shine. The following graphics show the time between sunrise and noon on the horizontal axis. The time for sunrise was deduced in Blog # 3, formula (11). We display the formula as time of day (analogous to τo ) : τrise = arccos(tan δ tan φ)/15° |
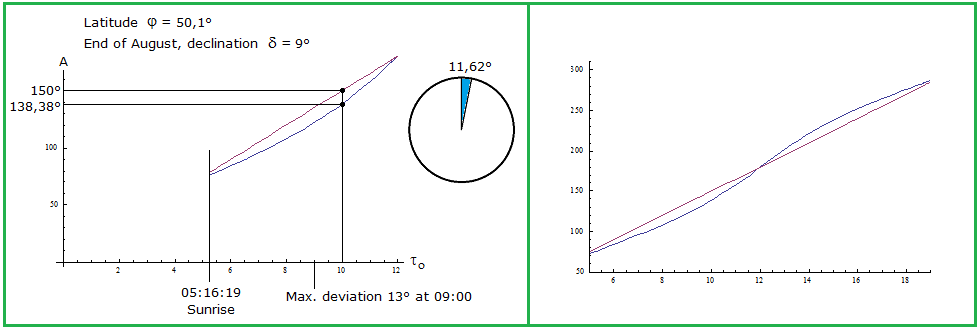
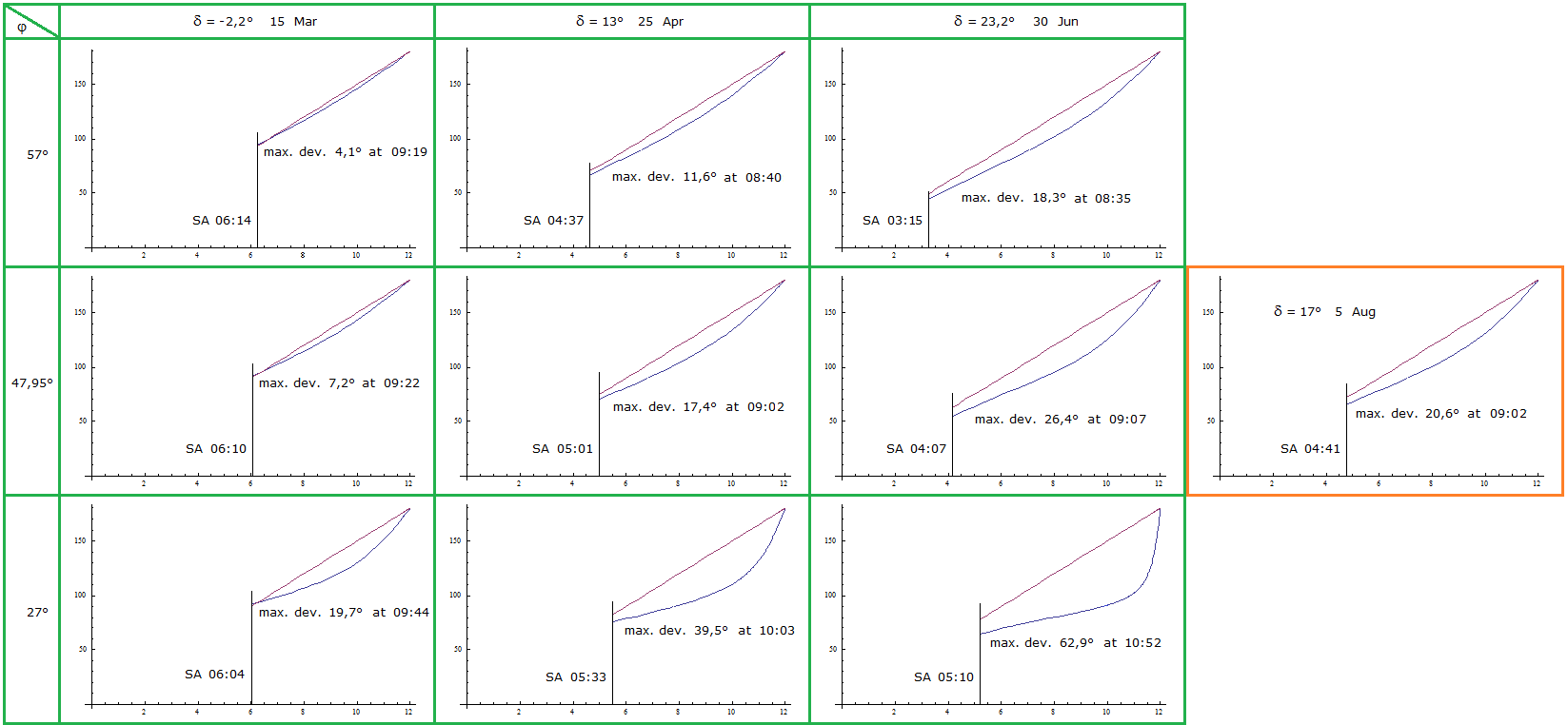
Copyright figure 1
Source and Author
Creative Commons BY-SA 3.0
back to figure 1
Published 2021-10-25 last update 2021-01-18