MB Matheblog # 44

Inhalt Blog voriger Eintrag

zur Leitseite Index der gesamten Website

2025-10-30                    Kommentare sind willkommen. Der kleine Prinz

english version

Der kleine Prinz ist bekannt aus dem Buch von Antoine de Saint-Exupéry, aus dem auch das Bild oben rechts entnommen wurde.

Der kleine Prinz steht auf einem Planeten. Dieser Blogbeitrag widmet sich der folgenden Frage:

(*)   Welche Gestalt muss der Planet haben, um die maximale Anziehungskraft auf den kleinen Prinzen auszuüben? An welcher Stelle des Planeten muss er dabei stehen?

Der Planet soll das Volumen \(_~V_~\) und die homogene Dichte \(_~d_~\) haben.

Wir stellen uns den Planeten im dreidimensionalen \(_~(x,y,z)-\)Raum vor. Der Koordinatenursprung \(_~(0,0,0)_~\) sei der Fußpunkt des kleinen Prinzen. Die \(_~z-\)Achse sei definiert durch seine Körperachse. Wir wollen nur Lösungen akzeptieren, bei denen der Planetenkörper den Koordinatenursprung berührt und bei denen die Kraft ausschließlich in \(_~z-\)Richtung wirkt.

Liegt ein Raumpunkt \(_~(x,y,z)_~\) im Planeten, so übt er nach dem Newton'schen Gravitationsgesetz auf den Fußpunkt des kleinen Prinzen in \(_~(0,0,0)_~\) eine vektorielle Anziehungskraft aus, die sich in Einzelwirkungen in \(_~x-,_{~~}y-_~\) und \(_~z-\)Richtung zerlegen lässt. Wir sind nur an der Kraft in \(_~z-\)Richtung interessiert. Diese Kraft beträgt \[\textbf{(1)}~~~~f_z=G\cdot d\cdot \frac{z}{(x^2+y^2+z^2)^{~3/2}}\] mit der Gravitationskonstanten \(~G~\).

Insgesamt  –  über den ganzen Planeten genommen  –  beträgt die Gravitationswirkung auf den kleinen Prinzen in \(_~z-\)Richtung also \[\textbf{(2)}~~~~F_z=\int_{V} f_z~dV\]

\(F_{z_~}\) wird mit der Einheit \(~m/s^2_~\) (\(m\): Meter, \(~s\): Sekunden) angegeben, da es sich um die Gravitationsbeschleunigung handelt. Dies wird sich auch weiter unten bei der numerischen Bestimmung von \(_~F_{z_~}\) ergeben.

Gesucht ist also diejenige Gestalt des Planeten, die \(_~F_{z_~}\) in (2) maximiert.

Die Maximaleigenschaft lässt den Schluss zu, dass der Planet vollständig im positiven \(_~z-\)Halbraum liegt. Denn ein Massenpunkt im negativen \(_~z-\)Halbraum hätte \(~f_z\lt 0_~\), siehe (1). Eine Verlagerung in den positiven \(_~z-\)Halbraum würde also \(_~F_{z_~}\) in (2) vergrößern.

Nun zum Kernpunkt der Argumentation für die Lösung von (*).  Wir werden zeigen, dass bereits die Wirkung von (1) auf der Oberfläche des Planeten genügend Information zur Lösung enthält, falls \(_~F_{z_~}\) maximal ist:

• \(f_{z_~}\) in (1) ist für \(_~(x,y,z)_~\) auf der Oberfläche des Planeten konstant. \[\textbf{(3)}~~~~\frac{z}{(x^2+y^2+z^2)^{~3/2}}=C_1\gt 0\]
• Begründung:  \(~A_1=(x_1,~y_1,~z_1)_~\) und \(_~A_2=(x_2,~y_2,~z_2)_~\) seien Oberflächenpunkte.
  Ann.  \(~f_z(A_1) \gt f_z(A_2)\).  Aus Stetigkeitsgründen gibt es dann \(_~\epsilon-\)Umgebungen \(_~U_{\epsilon}(A_1)\) und \(_~U_{\epsilon}(A_2)\) mit \(~f_{z_~}\vert _{U_{\epsilon}(A_1)}~\gt~f_{z_~}\vert _{U_{\epsilon}(A_2)}\).
  \(U_{\epsilon}(A_1)\) besteht zum Teil aus Leerraum; \(U_{\epsilon}(A_2)\) besteht zum Teil aus Planetenmaterie. Ein Materialtransfer aus \(U_{\epsilon}(A_2)\) in den Leerraum von \(U_{\epsilon}(A_1)\) vergrößert \(_~F_{z_~}\). Also war \(_~F_{z_~}\) vorher nicht maximal. Wid.


• Daraus folgt, dass der Planet rotationssymmetrisch ist, mit der \(_~z-\)Achse als Rotationsachse.
  • Begründung:  Wir betrachten die \(_~z_0-\)Ebene (Querschnitt parallel zur \(_~(x,y)-\)Ebene): An allen Randpunkten des Querschnitts ist \(_~{x^2+y^2}_~\) wegen (3) konstant (\(=r^2\)), bildet also einen Kreis mit \(_~(0,0,z_0)_~\) als Mittelpunkt.
  \[\textbf{(4)}~~~~\frac{z_0}{(r^2+{z_0}^2)^{~3/2}}=C_1\gt 0\]

Das Maximum von \(_~r(z)_~\) beträgt \(~\sqrt{2}\cdot (C/3)^{_~3/4}\)  und wird bei \(~z=(C/3)^{_~3/4}\)  angenommen.

Die folgende Skizze zeigt den Graphen von \(_~r(z)_~\) für \(_~C=1_~\). Dies ist die eine Hälfte der Randkurve des Planeten in einem Querschnitt, der die \(_~z-\)Achse enthält. Der kleine Prinz steht in negativer \(_~z-\)Richtung mit den Füßen im Koordinatenursprung.

Bemerkung: Mit der Herleitung von \(_~r(z)_~\) in (4) und (5) wird klar, dass der Planet keine Hohlräume aufweist.


Bild 1   \(_~r(z)_~\) für \(_~C=1_~\)

Die Gestalt der Kurve in Bild 1 hängt nicht von der Wahl von \(_~C_~\) ab. Man kann nämlich zeigen, dass sich jeder Graph von \(_~r(z)_~\) für ein beliebiges \(_~C_~\) durch eine gleichmäßige Skalierung in \(_~z-_~\) und \(_~r-\)Richtung zum Graphen für \(_~C=1_~\) transformieren lässt. Eine solche Ähnlichkeitstransformation wird für eine Funktion \(_~f(x)_~\) und den Skalierungsfaktor \(_~1/h_~\) beschrieben durch \[f(x)~~\rightarrow~~\frac{1}{h}~f_~(h\cdot x)\] Hier wählen wir \(_~h=C^{3/4}\) : \[r(z)_{~C}=\sqrt{C\cdot z^{2/3}-z^{2~}}~~~\rightarrow~~~\frac{1}{h}~\sqrt{C\cdot h^{2/3}\cdot z^{2/3}-h^{2~}\cdot z^{2~}}~=~C^{-3/4}\cdot \sqrt{C^{3/2}\cdot z^{2/3}-C^{3/2}\cdot z^2}~=~\sqrt{z^{2/3}-z^{2~}}~=~r(z)_{~C=1}\]
Wir vervollständigen die Kurve in Bild 1, drehen sie um \(_~90°_~\) im Uhrzeigersinn und heben die Einschränkung \(_~C=1_~\) auf:

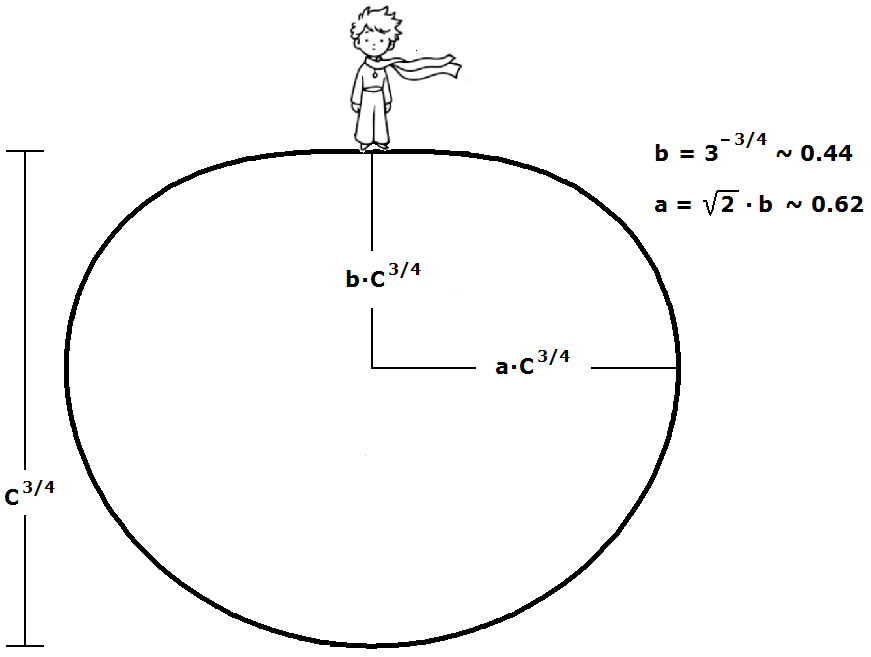
Bild 2   Querschnitt durch den Rotationskörper

Dieser Körper erfüllt die zwei Bedingungen, die wir anfänglich für eine gültige Lösung aufgestellt haben, nämlich dass der Körper den Fußpunkt des Prinzen berührt und dass die Kraft ausschließlich entlang seiner Körperachse wirkt (wegen der \(_~z-\)Rotationssymmetrie des Planeten).

Damit ist die Anfangsfrage (*) beantwortet. Der kleine Prinz steht am Ende der Rotationsachse auf der "stumpfen" Seite des Rotationskörpers wie in Bild 2.  –  Es wird jetzt gezeigt, wie \(_~C_~\) von \(_~V_~\) abhängt. Bei der folgenden Volumenberechnung wird benutzt, dass der Planet keine Hohlräume aufweist (s.o.). \[V=\int_0^{C^{3/4}}\pi\cdot r^2(z)~dz~=~\pi\int_0^{C^{3/4}}(_~C\cdot z^{2/3}-z^{2_~})~dz~=~\pi~\left[\frac{3~C}{5}~z^{5/3}-\frac{1}{3}z^{3_~}\right]_0^{C^{3/4}}~=~\frac{4_~\pi}{15}~C^{9/4}\] \[\textbf{(6)}~~~~C=\left(\frac{15_~V}{4_~\pi}\right)^{4/9}\]
Damit können wir nun \(_~{F_z}_~\) in Abhängigkeit von \(_~V_~\) und \(_~d_~\) berechnen. Mit (1) und (2) gilt: \[F_z~=~G\cdot d\cdot \int_{V} \frac{z}{(x^2+y^2+z^2)^{~3/2}}~dV\] Übergang zu Zylinderkoordinaten: \[F_z~=~G\cdot d\cdot \int_{0}^{C^{3/4}}\int_{0}^{\sqrt{Cz^{2/3}-z^2}}\int_{0}^{2_~\pi} \frac{z\cdot r}{(r^2+z^2)^{~3/2}}~d\phi~dr~dz\] \[~~~~~~=~2\cdot \pi\cdot G\cdot d\cdot \int_{0}^{C^{3/4}} \left[_~-\frac{z}{\sqrt{r^2+z^2}}~\right]_{r~=~0}^{r~=~\sqrt{Cz^{2/3}-z^2}}~dz\] \[~~~~~~=~2\cdot \pi\cdot G\cdot d\cdot \int_{0}^{C^{3/4}} \left(1-\frac{z^{2/3}}{\sqrt{C}}~\right)~dz\] \[~~~~~~=~2\cdot \pi\cdot G\cdot d\cdot \left[_~z-\frac{3}{5}\cdot \frac{z^{5/3}}{\sqrt{C}}_~\right]_{0}^{C^{3/4}}~=~\frac{4}{5}\cdot \pi\cdot G\cdot d\cdot C^{3/4}\] Mit (6) erhalten wir das Endergebnis: \[\textbf{(7)}~~~~F_z=\left(\frac{4_~\pi}{5}\right)^{2/3}G\cdot d\cdot (3_~V)^{1/3}\]
Zum Vergleich stellen wir den kleinen Prinzen auf einen kugelförmigen Planeten mit gleichem Volumen, gleicher Dichte und Radius \(_~R_~\). \(_~r^2~\) läuft dann im Intervall \(_~[_~0,~{R^2-(R-z)^2}_~]~=~[_~0,~{2_~R_~z_~-_~z^2}_~]\). \[F_{z~Kugel}~=~G\cdot d\cdot \int_{0}^{2_~R}\int_{0}^{\sqrt{2_~R_~z_~-_~z^2}}\int_{0}^{2_~\pi} \frac{z\cdot r}{(r^2+z^2)^{~3/2}}~d\phi~dr~dz\] \[~~~~~~=~2\cdot \pi\cdot G\cdot d\cdot \int_{0}^{2_~R} \left[_~-\frac{z}{\sqrt{r^2+z^2}}~\right]_{r~=~0}^{r~=~\sqrt{2_~R_~z_~-_~z^2}}~dz\] \[~~~~~~=~2\cdot \pi\cdot G\cdot d\cdot \int_{0}^{2_~R} \left(1-\sqrt{\frac{z}{2_~R}}~\right)~dz\] \[~~~~~~=~2\cdot \pi\cdot G\cdot d\cdot \left[_~z-\frac{2}{3}\cdot \frac{z^{3/2}}{\sqrt{2_~R}}_~\right]_{0}^{2_~R}~=~\frac{4}{3}\cdot \pi\cdot G\cdot d\cdot R\] Mit \(_~R=(3V/(4\pi))^{1/3}\) erhalten wir das Endergebnis: \[\textbf{(8)}~~~~F_{z~Kugel}=\left(\frac{4_~\pi}{3}\right)^{2/3}G\cdot d\cdot V^{1/3}\] Der Vergleich von (7) und (8) ergibt \(F_{z}/F_{z~Kugel}\approx 1,026_~\); der exakte Wert steht unten in der Zusammenfassung.

Der Vollständigkeit halber soll noch gezeigt werden, dass die Gravitationswirkung in \(_~x-_~\) und \(_~y-\)Richtung \(_~=0_~\) ist. In Zylinderkoordinaten ist \(~x=r\cdot cos~\phi,~~y=r\cdot sin~\phi_~\).  Sowohl für den Planeten des kleinen Prinzen als auch für die Kugel folgt \[F~_{x \atop y}=G\cdot d\cdot \int_{0}^{..} \int_{0}^{..} \int_{0}^{2_~\pi} \frac{r^2~{cos~\phi \atop sin~\phi}}{\sqrt{r^2+z^2}}~d\phi~dr~dz~=~G\cdot d\cdot \int_{0}^{..} \int_{0}^{..} \frac{r^2}{\sqrt{r^2+z^2}} \int_{0}^{2_~\pi} {cos~\phi \atop sin~\phi}~d\phi~dr~dz~=~G\cdot d\cdot \int_{0}^{..} \int_{0}^{..} \frac{r^2}{\sqrt{r^2+z^2}}\cdot 0~dr~dz~=~0\]

Beispiel

Hier sollen jetzt auch die physikalischen Einheiten einbezogen werden.

Für die Erde (als kugelförmig mit konstanter Dichte angenommen) und den oben beschriebenen Rotationskörper setzen wir \[V\approx 1,0833\cdot 10^{21}~m^3,~~~~d\approx 5,517\cdot 10^3~\frac{kg}{m^3},~~~~G\approx 6,6743\cdot 10^{-11}~\frac{N\cdot m^2}{kg^2}\] \[\Longrightarrow~~~F_z\approx 10,082~\frac{N}{kg}=10,082~\frac{m}{s^2}~,~~~~~F_{z~Kugel}\approx 9,827~\frac{N}{kg}=9,827~\frac{m}{s^2}\]
Die Wirtschaftswissenschaften kennen eine analoge Problemstellung: Das Equimarginalprinzip.

Dieses Prinzip wurde schon 1854 von Hermann Heinrich Gossen formuliert und kann als ein ökonomisches Axiom eingestuft werden. Das Equimarginalprinzip beschreibt, wie Ressourcen eingesetzt werden müssen, um einen maximalen Ertrag zu erzielen. Beim Kleinen Prinzen entsprechen die Massenpunkte des Planeten den Ressourcen und die Gravitationswirkung dem Ertrag.

Erläuterungen zum Equimarginalprinzip findet man auf Economics online.


Kategorie: Geomathematik                    Kommentare sind willkommen.

Stand 2025-07-03

Inhalt Blog   |    voriger Eintrag

Manfred Börgens   |   Zur Leitseite