2025-12-17 Kommentare sind willkommen.
Sportwetten
1. Sportwetten sind ein großer Markt. Im Internet findet man zahlreiche Anbieter für ein breites Spektrum von Wetten auf Sportereignisse. Wir wollen uns hier auf einfache Fußballwetten beschränken, aber die Prinzipien dieser Wetten, die im Folgenden untersucht werden sollen, lassen sich mühelos auf andere Wetten übertragen.
Die einfachen Fußballwetten erlauben dem Tipper, für ein Spiel einen Tipp auf 1, 0 oder 2 abzugeben; dies entspricht einem Tipp auf Heimsieg, Remis oder Auswärtssieg. Die Anbieter bieten Quoten für jeden dieser Spielausgänge an; eine Quote Q bedeutet, dass bei erfolgreicher Wette pro einsetztem Euro eine Gewinnauszahlung von Q Euro erfolgt; falls die Wette nicht erfolgreich war, also ein anderer Spielausgang stattgefunden hat, ist der Einsatz verloren.
In Bild 1 sieht man Screenshots für Quoten von drei Spielen und vier Anbietern. Die Layouts sind verschieden, aber der Aufbau ist vergleichbar.

Bild 1 2./3. Juli 2023 – 1. schwedische Liga
Beispiel für eine Quote: Wer beim Anbieter interwetten 10 Euro auf ein Remis im Spiel Halmstad - Göteborg gesetzt hat, erhält 31,50 Euro zurück, denn das Spiel endete 0:0 . Er hätte sich aber vorher über die Quoten der anderen Anbieter informieren sollen, denn bei bwin hätte er 32 Euro bekommen.
2. Hinter den Quoten stehen sowohl Wahrscheinlichkeiten für den Ausgang der Spiele als auch Gewinnmargen für die Anbieter. Wie werden die Quoten von den Anbietern berechnet? Am Anfang stehen immer vermutete Wahrscheinlichkeiten für den Ausgang der Spiele, die von Experten mit Unterstützung durch Algorithmen festgelegt werden. Für ein konkretes Spiel wollen wir diese Wahrscheinlichkeiten p1, p0 und p2 nennen, für Heimsieg, Remis und Auswärtssieg (Ereignisse E1, E0, E2) ; hier ist ein Beispiel:
p1 p0 p2
0,40 0,32 0,28
Der nächste Schritt ist die Bestimmung von fairen Quoten Ri :
R1 R0 R2
2,500 3,125 3,571
Diese Quoten sind fair, da sie als Reziproke der pi berechnet werden:
(1) Ri = 1/ pi
Dabei wird unterstellt, dass die pi die "wahren" Wahrscheinlichkeiten für die Ei sind. Der Erwartungswert für die Auszahlung bei 1 Euro Einsatz ist dann Ri·pi = 1 Euro. Nun möchte aber der Anbieter bei diesem Spiel etwas verdienen und pro eingesetztem Euro im Mittel nur 1-g Euro auszahlen; g ist die "Gewinnmarge". Dafür muss er nur die fairen Quoten mit 1-g multiplizieren und erhält mit (1) die "angebotenen" Quoten Qi :
(2) Qi = Ri ·(1-g) = (1-g)/ pi
Für unser Beispiel bedeutet das bei g = 0,07 ( 7 % Gewinnmarge des Anbieters):
pi 0,40 0,32 0,28
Ri 2,500 3,125 3,571
Qi 2,325 2,906 3,321
Die Qi sind die Quoten, wie sie beispielhaft in Bild 1 zu sehen sind. – Die Gewinnmarge g wird sich im Mittel für den Anbieter natürlich nur einstellen, wenn große Mengen von Tipps abgegeben werden und sich die von ihm geschätzten pi als weitgehend richtig erweisen.
Der Tipper kann nun aus den angebotenen Quoten Qi sowohl berechnen, welche Gewinnmarge g der Anbieter einbehält, als auch welche Wahrscheinlichkeiten pi für die Ei vom Anbieter geschätzt wurden (und er könnte evtl. zu einer ganz anderen Einschätzung kommen – das wird weiter unten noch diskutiert). Mit (2) geht das so:
1 = Σi pi = (1-g)· Σi 1/Qi ⇒
(3) g = 1 - 1 /(Σi 1/Qi)
(4) pi = (1-g)/ Qi
i durchläuft 1, 0, 2 für ein bestimmtes Spiel und einen bestimmten Anbieter. Wir wollen das beispielhaft anhand der bwin-Quoten für Halmstad - Göteborg aufzeigen:
Qi 2,37 3,20 2,95 → Bild 1
g 0,0684 → (3), siehe auch Bild 1
pi 0,393 0,291 0,316 → (4)
Der Tipper durchschaut also nun die Quoten des Anbieters, weil er g und pi kennt:
— Wenn der Anbieter mit seiner Einschätzung der pi richtig liegt, ist als Auszahlung an den Tipper pro eingesetztem Euro im Mittel 1-g = 0,9316 Euro zu erwarten.
— Der Tipper kann sich überlegen, ob er die pi plausibel findet oder ob er zu einer anderen Einschätzung kommt und dies ausnutzen möchte, um die erwartete mittlere Auszahlung 1-g zu übertreffen, vermutlich mit dem Ziel, dass diese > 1 ist. Wir kommen unten darauf zurück.
3. Soll man der eigenen Einschätzung des Spielausgangs vertrauen? Es ist zu vermuten, das viele Tipper, vielleicht sogar die Mehrheit, die Rechnungen unter Punkt 2. nicht durchführen, sondern sich auf ihr eigenes Gefühl verlassen. Das ist auch in Ordnung, denn: Es ist vollkommen egal, auf welchen Spielausgang man sein Geld setzt – jedenfalls wenn man den Wahrscheinlichkeiten der Experten glaubt. Denn im Mittel über viele Spiele verliert dann der Spieler g Euro pro eingesetztem Euro, und das gilt für jeden Tipp auf 1, 0 oder 2 .
Die eigene Einschätzung der Spielausgänge soll nun aber nicht völlig diskreditiert werden. Selbstverständlich darf man, zumindest bei einzelnen Spielen, anderer Meinung sein als die Experten. Lässt sich das evtl. gewinnbringend ausnutzen? Vielleicht – aber nicht so, wie es viele Tipper machen.
Nehmen wir an, ein Tipper setzt auf Heimsieg, weil er das für den wahrscheinlichsten Spielausgang hält. Man könnte ihn befragen, was denn seine persönlichen Wahrscheinlichkeiten sind:
1 mit Wahrscheinlichkeit 0,65
0 mit Wahrscheinlichkeit 0,2
2 mit Wahrscheinlichkeit 0,15
Also tippt er 1 . Das ist aber sinnlos. Er sollte sich statt dessen die Quoten anschauen. Da könnte z.B. ein Anbieter die Quoten 1,5 / 3,9 / 7,35 festlegen; das entspricht den Wahrscheinlichkeiten 0,629 / 0,242 / 0,128 , also gar nicht so unterschiedlich zum Tipper. Der Tipper hat somit folgende Erwartungswerte pro eingesetztem Euro: 0,975 / 0,78 / 1,1025 und sollte, auch wenn ihm das widersinnig erscheint, auf Auswärtssieg setzen.
4. Welche Wahrscheinlichkeiten für den Ausgang der Spiele sind realistisch? In Bild 2 sehen wir eine Tabelle, die in Zeile 1 die tatsächlichen Ergebnisse und in den Zeilen 3, 7, 11, 15 die Quoten Qi aus Bild 1 enthält. In den Zeilen 4, 8, 12, 16 stehen die zugehörigen Wahrscheinlichkeiten pi aus (4). Für jeden Anbieter und jedes Spiel wurde g , die Gewinnmarge des Anbieters, in den Spalten F, L, Q mit (3) berechnet.
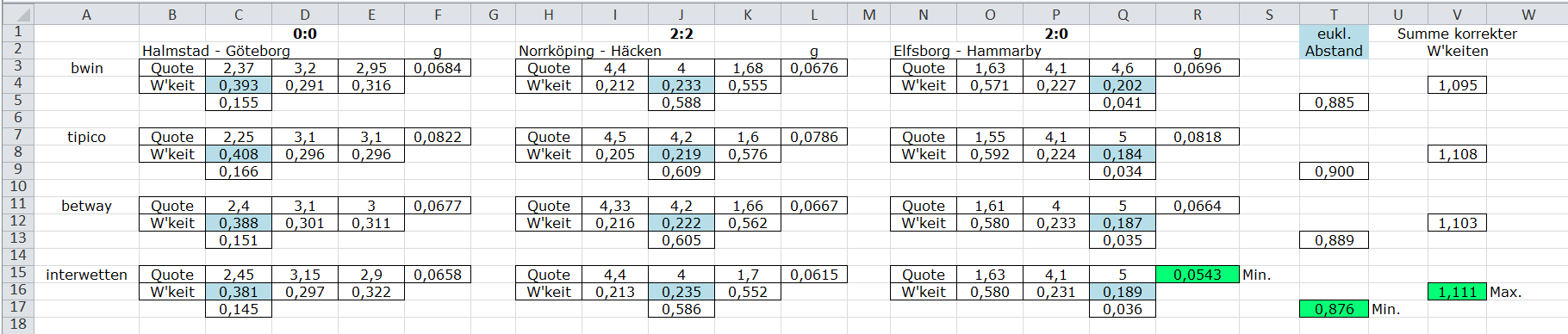
Bild 2
Nun gibt es verschiedene Möglichkeiten, diese Tabelle auszuwerten, um "eigene" oder "realistische" Wahrscheinlichkeiten festzulegen, die dem Tipper als Grundlage für seine Tipps dienen sollen.
a) Euklidischer Abstand der pi zu den Ergebnissen der Spiele. Für jeden Anwender soll eine Maßzahl für die Zuverlässigkeit der pi berechnet werden. Dazu wählt man eine große Anzahl von Spielen aus, deren Ergebnisse bereits bekannt sind, und nimmt bei jedem Spiel zufällig ein pi heraus (nur eines pro Spiel, da die pi innerhalb eines Spiel nicht unabhängig voneinander sind). In Bild 2 sind das die blau unterlegten Felder, also p1 für Halmstad - Göteborg, p0 für Norrköping - Häcken und p2 für Elfsborg - Hammarby. Pro Anbieter erhält man so einen Vektor von "a-priori-Wahrscheinlichkeiten". Dieser Vektor muss natürlich viel länger sein als in unserem Beispiel, um verlässliche Schätzungen der Zuverlässigkeit der pi zu bekommen. Dem "a-priori-Vektor" stellt man den "a-posteriori-Vektor" gegenüber, der sich aus den Spielergebnissen ergibt: Er enthält eine 1 an den Positionen, wo das Ereignis Ei eingetreten ist, und eine 0 sonst. In Bild 2 stehen die Ergebnisse in Zeile 1, so dass sich für den Anbieter bwin das folgende Bild ergibt:
a priori 0,393 0,233 0,202
a posteriori 0 1 0
Die vom Anbieter geschätzen pi sind tendenziell "gut", falls sie klein bei einer 0 (a posteriori) und groß bei einer 1 (a posteriori) sind. Deshalb liegt es nahe, den euklidischen Abstand EA der beiden Vektoren als Maßzahl für die Güte der pi zu nehmen:
a-priori-Vektor v , a-posteriori-Vektor w
(5) EA = ( Σj (vj - wj)2 )1/2
In Bild 2 stehen die Summanden (vj - wj)2 in den Zeilen 5, 9, 13, 17. Die zugehörigen EA stehen in Spalte T. Je kleiner ein solches EA ausfällt, desto näher lag die Einschätzung der Wahrscheinlichkeiten an den tatsächlichen Spielergebnissen. Dass hier der Anbieter interwetten am besten abgeschnitten hat, bedeutet gar nichts und soll das Verfahren nur beispielhaft beleuchten, denn drei Spiele sind viel zu wenig für eine sinnvolle Berechnung von EA .
So ergibt sich eine erste Möglichkeit für den Tipper, Wahrscheinlichkeiten als Grundlage seiner Tipps zu verwenden: Er vertraut auf die pi des Anbieters mit dem kleinsten EA . Er sollte die EA immer wieder anhand zahlreicher Spiele überprüfen.
b) Summe korrekter Wahrscheinlichkeiten. Es soll eine andere Maßzahl KW berechnet werden, die ebenfalls einen Vergleich der Anbieter erlaubt. Dazu addiert man bei vielen Spielen diejenigen pi eines Anbieters, die zum richtigen Ausgang der Spiele gehören. Je größer ein solches pi ist, desto besser wurde das zugehörige Spielergebnis vorhergesagt. Bei bwin stehen diese pi in Bild 2 in den Zellen D4, J4, O4 und die Summe KW in Zelle V4; Entsprechendes gilt für die anderen Anbieter. Auch hier liegt der Anbieter interwetten (rein zufällig!) am besten.
c) Mittelwerte der pi über die Anbieter. Falls sich mit a) und b) keine eindeutige Präferenz für einen Anbieter ergibt, kann man die gemittelten pi pro Spiel nehmen.
d) Eigene Wahrscheinlichkeiten. Ein Tipper, der von seiner eigenen Expertise überzeugt ist, kann die Wahrscheinlichkeiten für die Spielergebnisse selbst schätzen und die Verfahren a) und b) auf sich selbst anwenden und dann mit den Anbietern vergleichen – vielleicht ist er ja wirklich kompetenter.
5. Wie kann der Tipper seine Gewinnchancen maximieren? Wir haben gesehen, dass Sportwetten ein fast sicheres Verlustgeschäft sind. Das gilt zumindest dann, wenn häufig gespielt wird. Die mittlere erwartete Auszahlung pro eingesetztem Euro beträgt 1-g Euro, wobei g unterschiedliche Werte bei verschiedenen Anbietern annimmt (durchaus nennenswerte Unterschiede, siehe Bild 2!), und auch bei jedem einzelnen Anbieter schwankt g von Spiel zu Spiel (nicht sehr erheblich, siehe Bild 2). Insbesondere ist der Verlust des Spielers weitgehend unabhängig davon, auf welchen Spielausgang er sein Geld setzt.
Also ist es nicht unvernünftig, Anbieter mit niedrigem g zu bevorzugen. Das gilt jedenfalls dann, wenn man keine eigene Vorstellung von den Wahrscheinlichkeiten pi hat und auch keinen Vergleich der Anbieter bzgl. der Vorhersagequalität ihrer pi angestellt hat. Allerdings erscheint es sinnvoller, sein Augenmerk auf bestimmte einzelne Quoten zu lenken, um kleine Unterschiede zwischen den Anbietern auszunutzen und ggfs. auch die eigene Expertise gewinnbringend einfließen zu lassen.
Der erste Schritt wäre dann die Festlegung auf die vom Tipper verwendeten pi , also die Auswahl eines der Verfahren a) - d) in Abschnitt 4. Im zweiten Schritt multipliziert man diese pi mit den zugehörigen Quoten aller Anbieter und erhält für jeden Anbieter, jedes Spiel und jeden Spielausgang einen Erwartungswert für die Auszahlung. In Bild 3 wurde a), b) angewandt, d.h. in Zeile 2 wurden die pi des Anbieters interwetten aus Bild 2 zugrundegelegt.
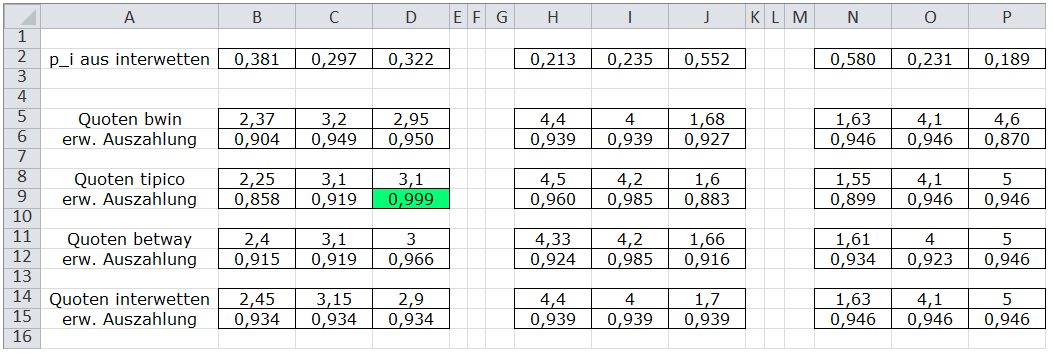
Bild 3 Die größten Erfolgsaussichten a priori verspricht ein Tipp beim Anbieter tipico auf Auswärtssieg im Spiel Halmstad - Göteborg. Diese Wette wäre allerdings verloren worden, denn das Spiel endete remis.
Würde der Tipper Verfahren c) verwenden, so würden sich die Erwartungswerte für die Auszahlungen in Bild 4 ergeben; sie sind die Produkte der Quoten mit den zugehörigen pi (gemittelte Wahrscheinlichkeiten aus Bild 2) in Zeile 2.

Bild 4 Die größten Erfolgsaussichten a priori verspricht ein Tipp beim Anbieter tipico auf Auswärtssieg im Spiel Halmstad - Göteborg. Diese Wette wäre allerdings verloren worden, denn das Spiel endete remis.
Bild 3 und Bild 4 zeigen, dass es einleuchtender ist, auf einzelne Quoten zu schauen als auf den Anbieter-Gewinn g . Wir wissen aus Bild 2, dass tipico bei den betrachteten Spielen der teuerste Anbieter ist, aber die grün markierten erwarteten Auszahlungen in den Bildern 3 und 4 legen dennoch nahe, einen Tipp bei diesem Anbieter abzugeben.
Eine lohnende zu erwartende Auszahlung, also ein Wert > 1 , findet sich nirgendwo in den Bildern 3 und 4. Das ist der Normalfall und liegt im Wesentlichen daran, dass sich die Anbieter bei den Quoten nur wenig unterscheiden.
Hinweis 1: Unterbewertete Unentschieden Bei den Quoten aller Anbieter fällt eine Merkwürdigkeit ist Auge. Bei zahlreichen Spielen wird ein "ausgeglichenes" Spiel erwartet; dies erkennt man daran, dass die Quoten für Heim- und Auswärtssieg nahe beisammen liegen. Bei ausgeglichenen Spielen würde man eine recht hohe Wahrscheinlichkeit für ein Unentschieden erwarten. Aber offenbar sehen die Anbieter das nicht so, denn in fast allen solchen Fällen hat das Remis die höchste Quote und damit die geringste Wahrscheinlichkeit, so wie im folgenden Beispiel:
Beispiel für ausgeglichenes Spiel:
3.7.2023 Allsvenskan (1. schwedische Liga), Anbieter bet-at-home
Mjällby - Kalmar
Qi 2,70 2,90 2,75
Offenbar waren die Experten bei bet-at-home der Meinung, dass es sich um ein schwer vorhersagbares Spiel handelt. Mit (3) berechnen wir g = 0,0731 und damit nach (4) die sehr ausgeglichenen Wahrscheinlichkeiten:
pi 0,343 0,320 0,337
Für geringe Remis-Wahrscheinlichkeiten bei ausgeglichenen Spielen mag es in einzelnen Fällen Gründe geben, aber die Anbieter handeln fast immer so (mit sehr seltenen Ausnahmen). Evtl. kann das ein Tipper zu seinen Gunsten ausnutzen und bevorzugt auf Remis tippen; das müsste natürlich im Langzeitversuch oder für eine große Zahl bereits gespielter Partien bestätigt werden. Das Spiel Mjällby - Kalmar endete übrigens 1:1 ; hier hätte sich also diese Überlegung ausgezahlt.
Hinweis 2: Niedrige Quoten auf Favoritensiege Tipper können beobachten, dass bei hohen Wahrscheinlichkeiten die Quoten nicht nur entsprechend klein, sondern zu klein sind. Auch das lässt sich evtl. im Langzeitversuch oder für eine große Zahl bereits gespielter Partien bestätigen. Der Grund dafür könnte daran liegen, dass die meisten Tipper auf den Favoriten tippen, statt die Quoten zu analysieren. Wenn nun ein Anbieter die bereits niedrigen Quoten für Favoritensiege etwas (aber nicht zu auffällig) heruntersetzt, gestaltet sich die zu erwartende Auszahlung für ihn noch etwas günstiger.
6. Fazit Sportwetten versprechen im Mittel über viele Spiele keinen Gewinn, sondern fast sicheren, aber moderaten Verlust. Sie machen nur Sinn als ein Spiel, bei dem der Spaß am Wetten die wesentliche Motivation ist. Dieser Spaß lässt sich durch mathematische Analysen steigern. Bei einem Anbieter, der 6 % der Einsätze einbehält, ist für einen regelmäßigen Tipper schon eine Rückzahlung von 97 % seiner Einsätze ein Erfolg, den er seinen Analysen verdankt.
Kommentare sind willkommen.
Stand 2023-07-13
Inhalt Blog | voriger Eintrag | nächster Eintrag
Manfred Börgens | Zur Leitseite
 MB Matheblog # 45
MB Matheblog # 45 MB Matheblog # 45
MB Matheblog # 45


