Dodekaeder    MB Matheblog # 33 Inhalt Blog
voriger Eintrag    nächster Eintrag		 zur Leitseite
Index der gesamten Website


2024-04-15                                                                 Kommentare sind willkommen.


Die Klothoide  –  eine Kurve für angenehmes Auto- und Bahnfahren


Kurven von Straßen und Bahntrassen sind problematischer als man denkt

In Bild 1 sehen wir zwei Geradenstücke, die sich im Winkel \(~\alpha~\) schneiden. Wir denken dabei an Straßen oder Bahngeleise. Für eine glatte Durchfahrung wird über dem Schnittpunkt eine Kurve angelegt. Wählt man diese Kurve als passenden Kreisbogen (Teilstück eines Kreises) mit Radius \(~R~\),  kann der gesamte Trassenverlauf als Graph einer differenzierbaren Funktion dargestellt werden. "Passend" bedeutet hier, dass an den Übergangspunkten Gerade/Kreis und Kreis/Gerade die Tangentensteigungen übereinstimmen. Dies ist in der rechten Graphik von Bild 1 dargestellt. Die Koordinatenachsen wurden so gewählt, dass der Anfang des Kreisbogens im Koordinatenursprung liegt; der Kreismittelpunkt ist dann \((0,~R)\).

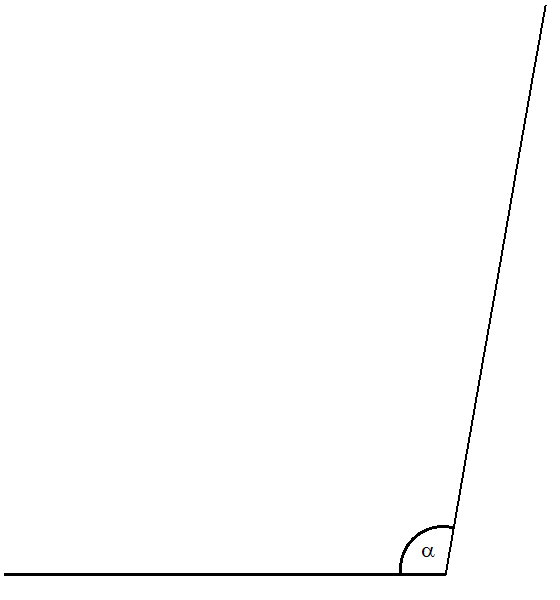
2 Straßen            Kreiskurve

Bild 1   Modellierung einer Kurve mittels eines Kreisbogens


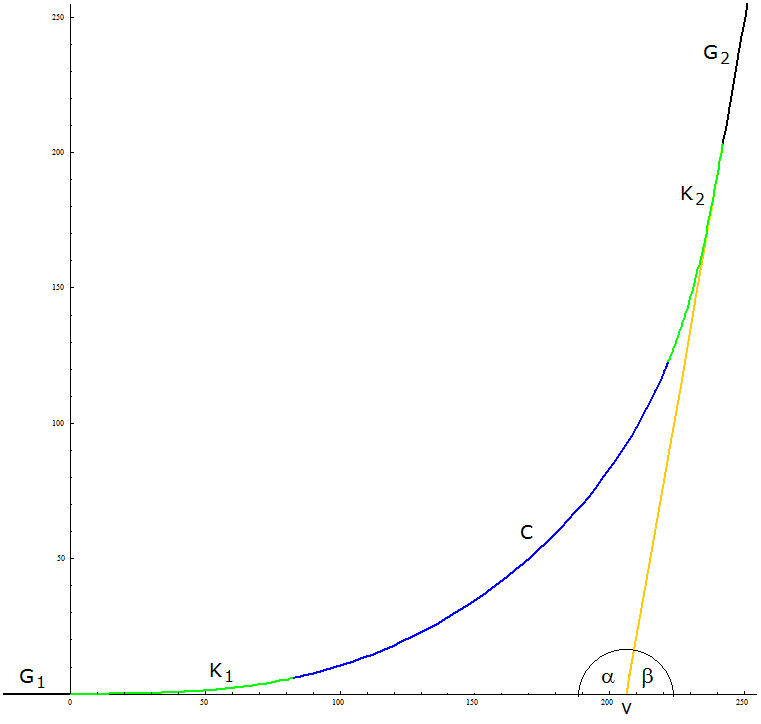
Trassenberechnung für den Kreisbogen

Eingabe: \(~\alpha~\) Winkel zwischen den Geraden    \(~R~\) Kreisradius

Parametrisierung für den Kreis  (Gegenuhrzeigersinn; Start in \((0,0))\) : \[(x,~y)=(R~\text{sin}~t,~R-R~\text{cos}~t)~~~~~~~~t~\in~(0,~\beta)~~~~\text{mit}~~~\beta = 180°-\alpha\] (1)  Fußpunkt der zweiten Geraden: \(~v_c=R~\text{cot}~\alpha/2\)

Übergang vom Kreisbogen in zweite Gerade: \((x,~y)=(R~\text{sin}~\beta,~R-R~\text{cos}~\beta)\)


Die hier vorgestellte Modellierung der Kurve mittels eines Kreisbogens erscheint wegen der sich stetig ändernden Tangentensteigung als einfach und günstig. Für Straßen, auf denen mit geringer Geschwindigkeit gefahren wird, ist dies eine brauchbare Lösung. Das gilt jedoch nicht für Schnellstraßen und erst recht nicht für Bahntrassen. Der Grund dafür liegt in der Krümmung der Trasse. Diese wird im nächsten Abschnitt eingehender behandelt; hier reicht es aus, sich vorzustellen, dass beim Autofahren die Krümmung der Fahrbahn proportional zum Lenkradeinschlag ist. Auf gerader Strecke ist die Krümmung konstant \(=0~\),  im Kreis konstant \(=1/R~\) (je kleiner der Kreis, desto größer die Krümmung).

Der Kreisbogen als Kurve erfordert also einen "Sprung" in der Lenkeinstellung beim Kurvenbeginn und -ende. Beim Autofahren kann man dem durch Ausweichen von der Ideallinie begegnen, aber das wird bei schnellem Fahren als unangenehm empfunden. Die Eisenbahn kann nicht von den Gleisen ausweichen und reagiert deshalb noch empfindlicher auf Unstetigkeiten im Krümmungsverlauf der Trasse. Im nächsten Abschnitt wird erklärt, wie man dieses Problem lösen kann.


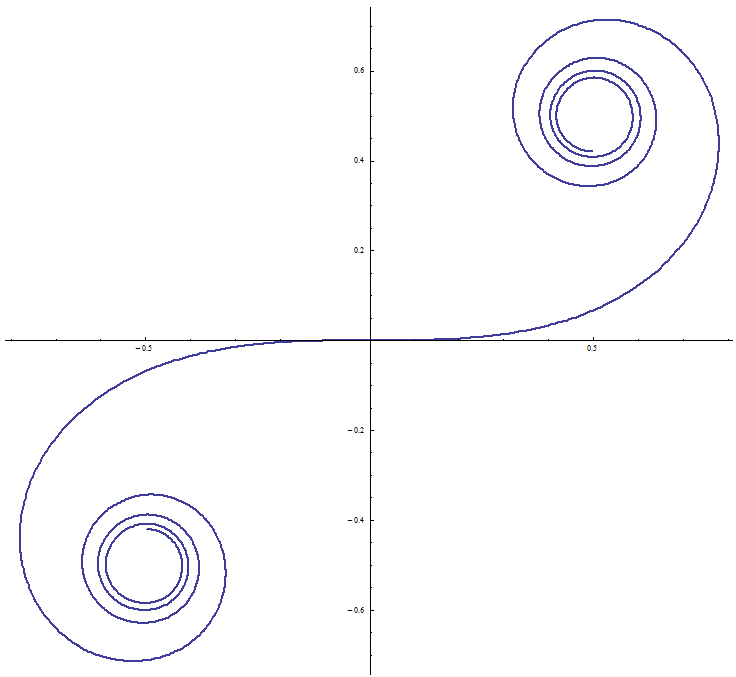
Die Klothoide als Lösung des Problems

Für ebene und zweimal differenzierbare Parameterkurven \((x(t),~y(t))\) wird die Krümmung definiert durch \[k(t) = \frac{x'(t)~y''(t)-x''(t)~y'(t)}{(x'(t)^2+y'(t)^2)^{3/2}}\] Ist \(~k(t)\) positiv, spricht man von einer Linkskrümmung, ist \(~k(t)\) negativ, von einer Rechtskrümmung (das entspricht den Links- und Rechtskurven beim Auto- oder Bahnfahren).

Geraden haben eine Krümmung \(=0~\),  Kreise eine konstante, zum Radius \(~R~\) reziproke absolute Krümmung \(|k(t)| = 1/R~\).

Der Krümmungskreis im Kurvenpunkt \(~T=(x(t_0),~y(t_0))\) ist der Kreis durch diesen Punkt mit Radius \(~R=1/|k(t_0)|~\) mit gleicher Tangente wie die Parameterkurve (grüne Kurve in Bild 2); die Normale in \(~T~\) in Richtung des Mittelpunkts \(~M~\) des Krümmungskreises muss dabei auf der konvexen Seite der Parameterkurve liegen.

Kruemmungskreis

Bild 2   Krümmungskreis

Für den Verkehr gilt: Kurven sollten keine Unstetigkeiten der Krümmung aufweisen. Bei Straßen wird man das vor allem bei Fernstrecken berücksichtigen, auf denen schnell gefahren wird. Bei Eisenbahntrassen hat man gar keine Wahl: Wenn sich die Krümmung nicht kontinuierlich ändert, handelt man sich ein Unfallrisiko (Entgleisung) ein.

Eine Zusammensetzung von Geradenstücken und Kreisbögen wie im vorigen Abschnitt kommt also nicht in Frage. Deshalb sucht man nach Kurven, deren Krümmung \(~k~\) stetig wächst, beginnend mit \(~k=0~\) (wie bei der Geraden) bis zu derjenigen Krümmung, die der vorgesehene Kreisbogen aufweist, also \(~|k|=1/R~\).  Eine dieser Kurven heißt Klothoide. Sie beruht auf den normalisierten Fresnel-Integralen \(~f_c~\) und \(~f_s~\): \[f_c(u)=\int_0^u \text{cos}~\frac{\pi~t^2}{2}~dt~~~~~~~~~~f_s(u)=\int_0^u \text{sin}~\frac{\pi~t^2}{2}~dt\] Die Fresnel-Integrale werden zu einer Parameterkurve, der Fresnel-Spirale, zusammengesetzt: \[(x,~y)=~(f_c(u),~f_s(u))~~~~~~~u \in \textbf{R}\] Klothoide

Bild 3   Fresnel-Spirale \((f_c(u),~f_s(u))\) für \(~u \in (-4,~4)\)

Die Klothoide ist eine Fresnel-Spirale mit dem Skalierungsfaktor \(~a~\sqrt{\pi}~\) zur Streckung oder Stauchung; außerdem wird der Parameter \(~u~\) durch \(~l~/~(a\sqrt{\pi})~\) substituiert und \(~l~\) als neuer Parameter gewählt (dies wird weiter unten noch begründet): \[\textbf{(2)}~~~(x,~y)=(x(l),~y(l))=a~\sqrt{\pi}~\left(f_c\left(\frac{l}{a~\sqrt{\pi}}\right),~f_s\left(\frac{l}{a~\sqrt{\pi}}\right)\right)~~~~~~~l \in \textbf{R}\] Das Bild von \(~(x(l),~y(l))~\) ist bis auf die Skalierung das gleiche wie in Bild 3.

(2) lässt sich mittels Substitution auch einfacher schreiben als \[\textbf{(3)}~~~(x(l),~y(l))=\left(\int_0^l \text{cos}~\frac{t^2}{2~a^2}~dt,~\int_0^l \text{sin}~\frac{t^2}{2~a^2}~dt\right)\] (2) hat gegenüber (3) den Vorteil, dass \(~f_c~\) und \(~f_s~\) mit Programmiersprachen (z.B. mit Mathematica) direkt evaluiert werden können.

Es gibt auch andere Parametrisierungen der Klothoide. (2) wurde in Hinblick auf die Anwendung im Straßen- und Eisenbahnbau gewählt (siehe nächster Abschnitt); insbesondere ist hier der Parameter \(~l~\) identisch mit der Kurvenlänge.  –  In den Quellen [1] - [4] (s.u.) werden die Eigenschaften der Klothoide hergeleitet. Eine Zusammenfassung gibt der folgende Kasten.


Klothoide
\[(x,~y)=(x(l),~y(l))=a~\sqrt{\pi}~\left(f_c\left(\frac{l}{a~\sqrt{\pi}}\right),~f_s\left(\frac{l}{a~\sqrt{\pi}}\right)\right)~~~~~~~l \in \textbf{R}\] Eigenschaften:
  • Doppelspirale, punktsymmetrisch zu \((0,0)\), siehe Bild 3

  • Der Parameter \(~l~\) ist die Länge der Kurve; genauer:

    \(s(l)~\) sei die Kurvenlänge von \((0,0)\) bis \((x(l),~y(l))\). Dann gilt:

    \(\textbf{(4)}~~~s(l)=l\)

  • Die Krümmung \(~k(l)\) im Punkt \((x(l),~y(l))\) beträgt: \[\textbf{(5)}~~~k(l)= \frac{l}{a^2}\] Die Krümmung wächst somit linear mit der Kurvenlänge \(~l~\).

  • Der Steigungswinkel \(~\tau(l)\) im Punkt \((x(l),~y(l))\) beträgt: \[\textbf{(6)}~~~\tau(l)= \frac{l^2}{2~a^2}\]

Zur numerischen Evaluation der Klothoide benutzte man früher Tabellenwerke, heute verwendet man in der Regel ein Programm. Sie lässt sich beispielsweise mit Mathematica leicht mittels

\(f_c(u)=\) FresnelC[u],   \(~f_s(u)=\) FresnelS[u]

berechnen. Man kann aber auch die sehr schnell konvergierenden Potenzreihen verwenden:

\[x(l)=l \cdot \sum_{n=0}^\infty (-1)^n~\frac{(l/a)^{4n}}{(2n)!~(4n+1)~4^n}\] Nenner           1
                40
             3.456
           599.040
       175.472.640
               ... \[y(l)=\frac{l}{2} \cdot \sum_{n=0}^\infty (-1)^n~\frac{(l/a)^{4n+2}}{(2n+1)!~(4n+3)~4^n}\] Nenner           3
               168
            21.120
         4.838.400
     1.765.048.320
               ...

Zur schnellen Konvergenz trägt bei, dass in den Anwendungen (siehe nächster Abschnitt) \(~l/a < 1~\) ist.



Die Klothoide als Übergangskurve

Wie machen es die Ingenieure im Straßen- und Eisenbahnbau, wenn bei Kurven eine stetige Änderung der Krümmung erforderlich ist? Die Kurve wird auch dann in ihrem Mittelteil meist entlang eines Kreisbogens verlaufen; aber beim Übergang Gerade/Kreis wird ein Stück der Klothoide eingefügt, so dass sich die Abfolge Gerade - Klothoide - Kreis - Klothoide - Gerade ergibt. Von der Klothoide, die der Doppelspirale in Bild 3 ähnlich ist, wird dabei in der Regel nur kleines Stück rechts von \(~0~\) verwendet.

Es gibt auch anspruchsvollere Modellierungen von Trassen, etwa wenn die Krümmung der Klothoide nicht bei \(~0~\) beginnen soll, sondern bei einem positiven Wert, weil dort eine andere Kurve einmündet. Solche weiterführenden Aufgabenstellungen basieren aber im Wesentlichen auf dem hier vorgestellten Problem; wenn dieses verstanden worden ist, wird der Sinn der Verwendung von Klothoiden hinreichend klar.

Vorgegeben werden der Winkel \(~\alpha~\) zwischen den geraden Straßen, der Kreisradius \(~R~\) und die Länge \(~L~\) der einzelnen Klothoiden.


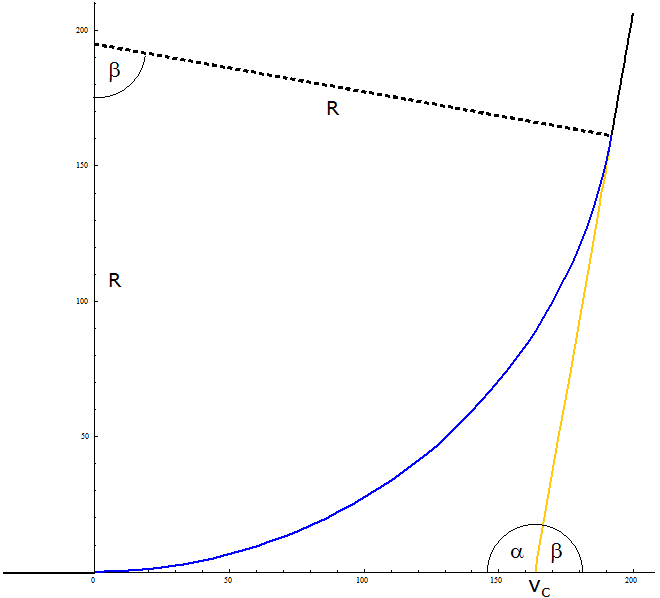
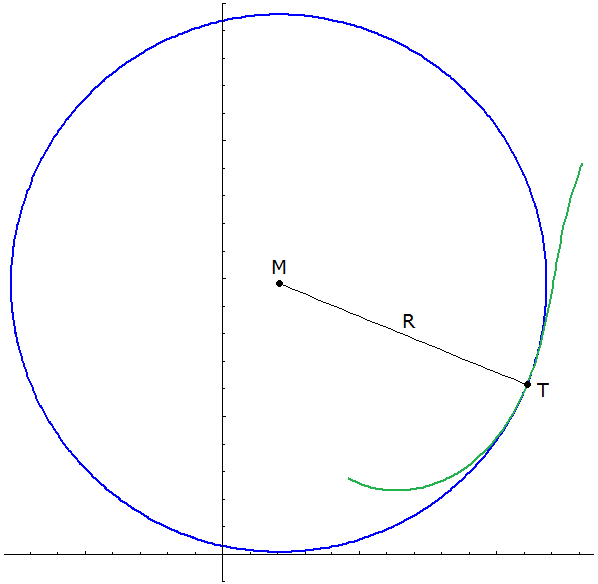
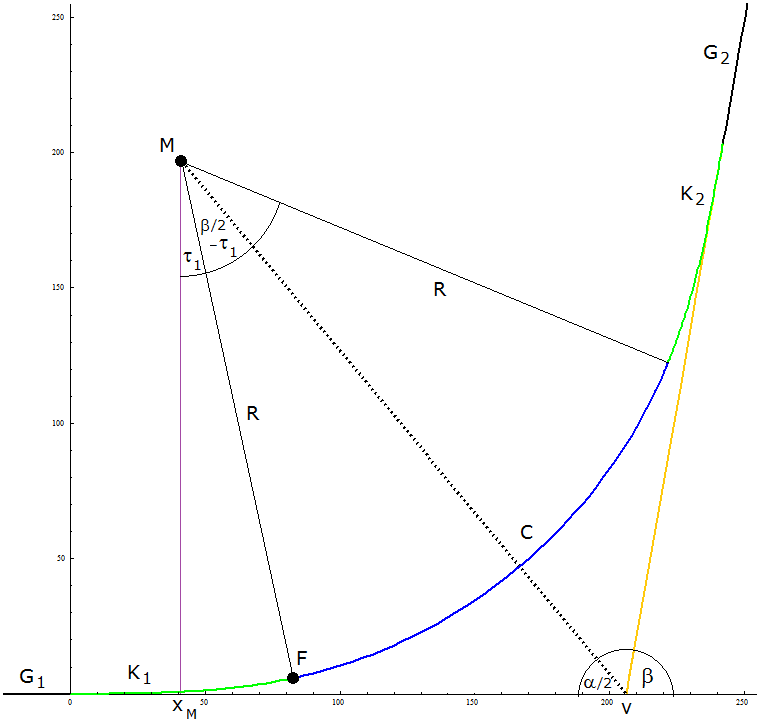
Berechnung der Kurve Klothoide - Kreisbogen - Klothoide  (siehe Bild 4)

Eingabe:  \(~\alpha~\) Winkel zwischen den Geraden

Eingabe:  \(~R~\) Kreisradius

Eingabe:  \(~L~\) Länge eines Klothoidenabschnitts zwischen Gerade und Kreis

Beim Übergang Klothoide - Kreis stimmen die Tangenten überein, da es sich um den Krümmungskreis am Ende der Klothoide handelt. Die Klothoidenkrümmung beträgt nach (5) \(~L/a^2~\),  die Kreiskrümmung \(~1/R~\).  Diese Krümmungen müssen übereinstimmen. Daraus ergibt sich, welcher Faktor \(~a~\) in (2) bei der Klothoide eingesetzt werden muss: \[\textbf{(7)}~~~a=\sqrt{L\cdot R}\] \[\textbf{(8)}~~~~~~\rightarrow~~~K_1~:~~(x_1(l),~y_1(l))=\sqrt{\pi\cdot L\cdot R}~\left(f_c\left(\frac{l}{\sqrt{\pi\cdot L\cdot R}}\right),~f_s\left(\frac{l}{\sqrt{\pi\cdot L\cdot R}}\right)\right)~~~~~~~l \in (0,~L)\] Die Parametrisierung des Kreises soll im Gegenuhrzeigersinn erfolgen und mit Tiefpunkt bei \(~t=0~\): \[\textbf{(9)}~~~C~:~~(x_c(t),~y_c(t))=(x_M+R~\text{sin}~t,~y_M-R~\text{cos}~t)~~~~~~~t \in [~\tau_1,~\tau_2~]\] Hierfür sollen im Folgenden das Definitionsintervall \(~[~\tau_1,~\tau_2~]~\) für den Parameter \(~t~\) sowie der Kreismittelpunkt \(~M=(x_M,~y_M)\) bestimmt werden.

Steigungswinkel im Punkt \(~F~\) beim Übergang \(~K_1 - C~\) nach (6), (7): \[\textbf{(10)}~~~\tau_1= \frac{L^2}{2~a^2}= \frac{L}{2~R}\] \(t=\tau_1~\) ist auch der "Startwinkel" für \(~C~\).

Der halbe Innenwinkel bei \(~M~\) für \(~C~\) beträgt \(~90°-\alpha/2-\tau_1 = \beta/2-\tau_1~\).  Damit ergibt sich, bei welchem Winkel \(~t=\tau_2~\) der Kreisbogen \(~C~\) beim Übergang \(~C - K_2~\) endet: \(~\tau_1+2~(\beta/2-\tau_1)~\).  Also gilt: \[\textbf{(11)}~~~\tau_2= \beta - \tau_1\] Berechnung von \(~M~\) mit (9): \(~~~~~x_M+R~\text{sin}~\tau_1 = x_1(L)~~~~~~~~~y_M-R~\text{cos}~\tau_1 = y_1(L)\) \[\textbf{(12)}~~~~~~\rightarrow~~~x_M = x_1(L)-R~\text{sin}~\tau_1~~~~~~~~~y_M = y_1(L)+R~\text{cos}~\tau_1\] \(\textbf{(13)}~~~\)Fußpunkt von \(~G_2:~~v=x_M+y_M ~\text{cot}~\alpha/2\)

\(K_2~\) erhält man durch Spiegelung (*, s.u.) von \(~K_1~\) an der Winkelhalbierenden von \(~\alpha~\): \[\textbf{(14)}~~~K_2~:~~(x_2(l),~y_2(l)) = ((x_1(l)-v)~\text{cos}~\alpha - y_1(l)~\text{sin}~\alpha+v,~-(x_1(l)-v)~\text{sin}~\alpha - y_1(l)~\text{cos}~\alpha)~~~~~~~l \in (0,~L)\] Mit (13) erhält man die Gleichung der zweiten Geraden: \[\textbf{(15)}~~~G_2~:~~y = (x-v)~\text{tan}~\beta~~~~~~~x \ge x_2(L)\]

Zu (*): Spiegelung eines Punktes \((x,~y)\) an der Geraden durch \((x_0,~y_0)\) mit Steigungswinkel \(~\gamma~\): \[\left( \begin{array}{c} x_{\text{gespiegelt}}\\ y_{\text{gespiegelt}}\\ \end{array} \right) = \left( \begin{array}{cc} \text{cos}~2~\gamma & \text{sin}~2~\gamma\\ \text{sin}~2~\gamma & -\text{cos}~2~\gamma\\ \end{array} \right)\cdot \left( \begin{array}{c} x-x_0\\ y-y_0\\ \end{array} \right)+ \left( \begin{array}{c} x_0\\ y_0\\ \end{array} \right) \] In (14) ist \(~\gamma = 180° - \alpha/2~\) und \[\left( \begin{array}{c} x\\ y\\ \end{array} \right)= \left( \begin{array}{c} x_1(l)\\ y_1(l)\\ \end{array} \right),~~~ \left( \begin{array}{c} x_{\text{gespiegelt}}\\ y_{\text{gespiegelt}}\\ \end{array} \right)= \left( \begin{array}{c} x_2(l)\\ y_2(l)\\ \end{array} \right)~~~\text{und}~~~ \left( \begin{array}{c} x_0\\ y_0\\ \end{array} \right) = \left( \begin{array}{c} v\\ 0\\ \end{array} \right) \]

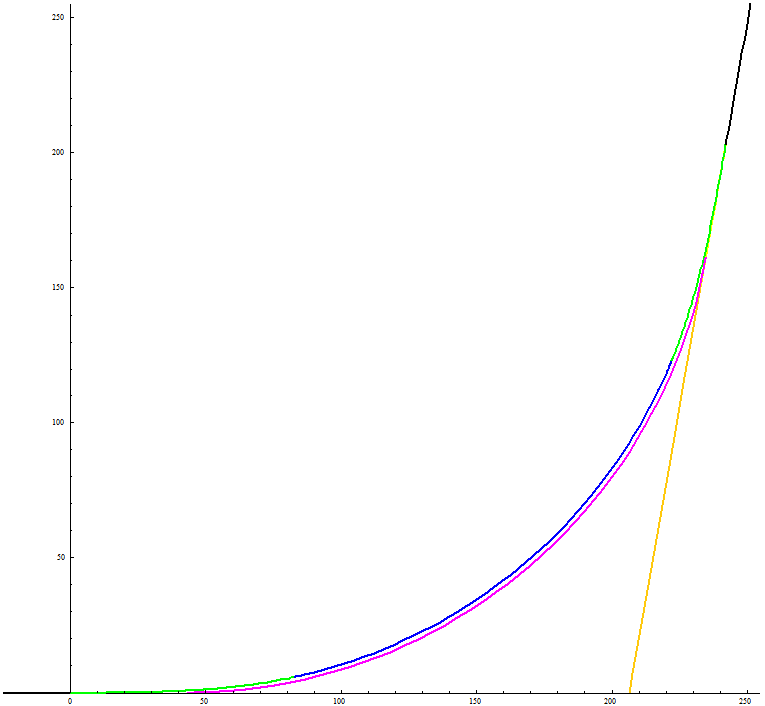
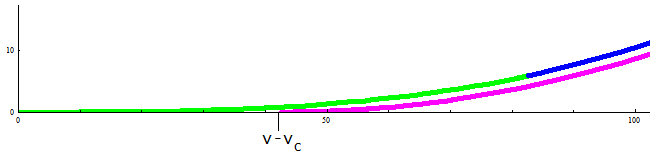
Trassenführung

Man berechnet zuerst \(~K_1,~\tau_{i~},~M~\) und \(~v~\) mit (8), (10), (11), (12), (13). Mit (8), (9), (14), (15) hat man dann alle Angaben, um die Trasse zeichnen und im Gelände abstecken zu können: \[G_1~:~~y = 0~~~~~~~x \le 0\] \[K_1~:~~(x_1(l),~y_1(l))~~~~~~~l \in (0,~L)\] \[C~:~~(x_c(t),~y_c(t))~~~~~~~t \in [~\tau_1,~\tau_2~]\] \(K_2~:~~(x_2(l),~y_2(l))~~~~~~~l \in (0,~L)~~~\)(eigentlich\(~l\in (L,~0)~~\)wegen der Durchlaufrichtung) \[G_2~:~~y = (x-v)~\text{tan}~\beta~~~~~~~x \ge x_2(L)\]


Wie unterscheidet sich die Trassenführung mit Klothoiden in Bild 4 von derjenigen ohne Klothoiden in Bild 1? In Bild 4 liegt der Schnittpunkt der beiden Geraden bei \(~x=v~\),  in Bild 1 bei \(~x=v_c~\).  Um beide Kurven in ein Koordinatensystem legen zu können, verschieben wir den Kreisbogen aus Bild 1 um \(~v-v_c~\) nach rechts. Das Ergebnis sieht man in Bild 5. Die Trassen unterscheiden sich in der Skizze nur wenig, aber erheblich im Fahrkomfort.

Klothoiden und Ursprungskreis               Vergleich

Bild 5  Vergleich der Trassenführung mit und ohne Klothoiden. Der Kreisbogen aus Bild 1 ist hier violett gezeichnet und beginnt bei \(~v-v_c\).  –  Rechts sieht man einen vergrößerten Ausschnitt.



Beispiel

Vorgegeben sind \(~\alpha=100°,~R=195,~L=83~\);  diese Werte liegen den Graphiken in den Bildern 1, 4 und 5 zugrunde. Die Längenmaße kann man sich anschaulich als in Metern gemessen vorstellen. Im Folgenden sind die Gleichungen nicht exakt, sondern mit Rundungsfehlern behaftet. \[G_1~:~~y = 0~~~~~~~x \le 0\] \[~~~~~~~a = 127,2203\] \[K_1~:~~(x,~y)=(x_1(l),~y_1(l)) = 225,4921\cdot (f_c(0,004435\cdot l),~f_s(0,004435\cdot l))~~~~~~~l \in (0,~83)\] \[~~~~~~~\tau_1=12,1937°~~~~~~~\tau_2 = 67,8063°\] \[~~~~~~~M=(x_M,~y_M)=(41,4374,~~196,4696)\] \[~~~~~~~v=206,2950\] \[C~:~~(x,~y)=(41,4374+195~\text{sin}~t,~196,4696-195~\text{cos}~t)~~~~~~~t \in [~12,1937°,~67,8063°]\] \(K_2~:~~(x,~y) = (x_2(l),~y_2(l)) = (-0,1736 \cdot x_1(l) - 0,9848 \cdot y_1(l) + 242,1178,~~-0,9848 \cdot x_1(l) + 0,1736 \cdot y_1(l) + 203,1609)~~~~~~~l \in (0,~83)~~~\)
                     (eigentlich\(~l\in (83,~0)~~\)wegen der Durchlaufrichtung) \[G_2~:~~y = 5,6713~x-1169,9571~~~~~~~x \ge 242,1178\] \(~~~~~~~\)Öffnungswinkel für \(~C~\) (bei \(~M~\)) :\(~~~~\tau_2 - \tau_1~=~55,6126°\)

\(~~~~~~~\)Übergangspunkte zwischen den Kurvenstücken mit Steigungswinkeln: \[~~~~~~~G_1 - K_1~~~~~(0,~0)~~~~~0°\] \[~~~~~~~K_1 - C~~~~~~~(82,6249,~~5,8690)~~~~~12,1937°\] \[~~~~~~~C - K_2~~~~~~~(221,9903,~~122,8105)~~~~~67,8063°\] \[~~~~~~~K_2 - G_2~~~~~(242,1178,~~203,1656)~~~~~80°\] \(~~~~~~~\)Start- und Endpunkt der Kurve ohne Klothoiden, aber im selben Koordinatensystem; mit Steigungswinkeln: \[~~~~~~~(42,6706,~~0)~~~~~0°~~~~~~~~~~~(234,7081,~~161,1386)~~~~~80°\] Potenzreihen für die Klothoide: \[x(l)=\sum_{n=0}^\infty (-1)^n~\frac{l^{4n+1}}{(2n)!~(4n+1)~1.047.816.900^n}\] \[y(l)=\frac{1}{32.370} \cdot \sum_{n=0}^\infty (-1)^n~\frac{l^{4n+3}}{(2n+1)!~(4n+3)~1.047.816.900^n}\] Die ersten drei Summanden reichen aus, um die Klothoide mit hoher Genauigkeit zu berechnen.





Quellen

[1]  E. Bachmann: Die Klothoide als Übergangskurve im Straßenbau, in: Schweizerische Zeitschrift für Vermessung, Kulturtechnik und Photogrammetrie 49 (1951), Heft 6, S. 133 - 140

[2]  B. Frassek: Klothoide (Cornu-Spirale), in: 2D Mathe (Website)

[3]  U. Mende: Die Klothoide  –  und warum Straßenkurven keine Kreisbögen sind, in: Interessantes aus Mathematik und Physik 2020-04-14 (Website)

[4]  Wikipedia: Definition der Klothoide mittels Fresnelscher Integrale



Kommentare sind willkommen.


Stand 2023-03-02

Inhalt Blog   |    voriger Eintrag   |    nächster Eintrag

Manfred Börgens   |   Zur Leitseite