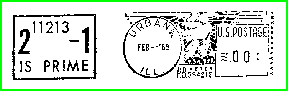Stempel des Monats Februar 2002

Vor 25 Jahren wurde der Vierfarbensatz bewiesen.

An der University of Illinois in Urbana war man Anfang 1977 mächtig stolz, denn an dieser Hochschule war Kenneth Appel, Wolfgang Haken (ein Deutscher aus Berlin) und John Koch ein sehr bemerkenswerter Beweis gelungen.

1852 machte Francis Guthrie die mathematische Welt auf seine (aus der Erfahrung gewonnene) Vermutung aufmerksam, dass man alle Landkarten mit nur vier Farben so einfärben kann, dass benachbarte Länder nicht die gleiche Farbe haben. Dieser "Vierfarbensatz" widerstand exakt 125 Jahre allen Beweisversuchen, bis Appel, Haken und Koch der Beweis gelang. Die University of Illinois feierte dieses Ereignis mit dem abgebildeten Stempel.

Mein Kollege Professor Dr. Hartmut Siebert hat die abgebildete Karte zur Verfügung gestellt, wofür ich ihm herzlich danke. Er muss einer der Ersten gewesen sein, die diesen schönen Stempel erhalten haben, denn der Beweis war am 9. Februar 1977 (Poststempel) noch ganz jung.

Was macht den Beweis so interessant?

• Wir haben es mit einem Theorem zu tun, das jeder sofort verstehen kann, das aber sehr schwer zu beweisen ist.
  
  
• Nur wenige prominente und leicht verständliche Probleme bleiben so lange ungelöst (wenn sie dann doch gelöst werden, gibt es großes Aufsehen, siehe etwa Fermats Letzter Satz).
  
  
• Appel, Haken und Koch bewiesen den Vierfarbensatz MIT HILFE DES COMPUTERS, und das war revolutionär (und schmeckt vielen Mathematikern bis heute nicht). Trotz mehrfacher Verbesserung der ursprünglichen Argumentation gibt es bislang keinen "klassischen" Beweis.

Hier ist eine 4-Färbung der deutschen Bundesländer, die zeigt, dass man mit drei Farben nicht auskommt (wegen Thüringen):



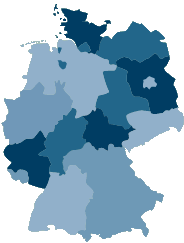
Man sollte sich klar machen, dass es keineswegs einfach ist, eine große Karte mit vier Farben einzufärben. Um dies einzusehen, können sich sportliche Leser dieser Seite z.B. an den französischen Departements versuchen:



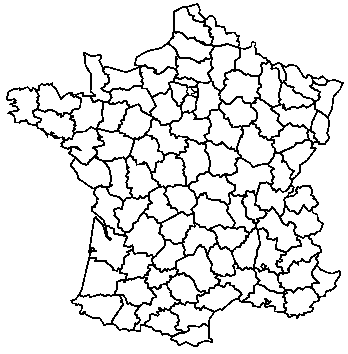
Der Vierfarbensatz gilt für alle Karten in der Ebene und auf dem Globus. Ein verblüffender Aspekt der Färbeprobleme ist, dass es analoge Sätze für das Möbiusband und den Torus gibt, die trotz der komplizierteren Form dieser Gebilde lange vorher bewiesen waren - und deren Beweise (vergleichsweise) mühelos anzugeben sind. Auf dem Möbiusband gilt der 6-Farben-Satz und auf dem Torus der 7-Farben-Satz. Die beiden folgenden Bilder zeigen, dass man tatsächlich nicht mit weniger Farben auskommt, da jeweils alle Farben gemeinsame Grenzen mit allen anderen haben:

Für Liebhaber der mathematischen Philatelie zeige ich noch einige andere Stempel. Der erste wurde mir freundlicherweise von meinem Kollegen Professor Dr. Ulrich Abel zur Verfügung gestellt.