China 2002   Michel 3384    Scott 3226   Mikronesien 1999   Michel 829    Scott 356

Liu Hui (ca. 220 - ca. 280)


Über das Leben des chinesischen Mathematikers Liu Hui ist nur wenig bekannt. Einen bedeutenden Platz in der Wissenschaftsgeschichte hat er sich erworben durch seine beiden Bücher. Sein Hauptwerk ist ein Kommentar der "Mathematik in neun Büchern" (engl. meist "Nine Chapters on the Mathematical Art", auf der Marke unten "Nine Chapter(s) on the Mathematics"). Das zweite Buch heißt "Mathematisches Handbuch für die Meeresinsel", das sich vorwiegend mit der Anwendung des Satzes von Pythagoras auf geographische Probleme befasst und seinen Namen von der Aufgabe bezieht, die Entfernung und die Höhe einer Insel im Meer zu berechnen.

Auf der rechten Briefmarke haben sich ein paar Fehler eingeschlichen: Liu Huis Name ist in der Fußzeile falsch angegeben; dahinter fehlt das "s" in "chapters"; ganz oben muss es "refined" heißen.

Die Briefmarke zeigt mehrere Referenzen auf die "Mathematik in neun Büchern" (im folgenden kurz: "Neun Bücher"). Dieses Werk wurde einige Jahrhunderte vor Liu Hui geschrieben; das genaue Entstehungsdatum und der Autor sind unbekannt. Die "Neun Bücher" sind eine nach Themen geordnete Aufgabensammlung mit durchweg praktischen Bezügen zum Ingenieurwesen, Steuerwesen und Handel. Liu Huis Leistung besteht in einer sehr ausführlichen Kommentierung der Aufgaben, in der er die vorher fehlende mathematische Fundierung beiträgt. Für die Erklärung der rechten Briefmarke müssen wir zwei der "Neun Bücher" heranziehen: "Landvermessung" (1. Buch) und "Rechtwinklige Dreiecke" (9. Buch). Aus diesen beiden Büchern werden wir die folgenden Abschnitte zitieren, die einen Bezug zur Marke haben:

• Flächeninhalt des regelmäßigen Zwölfecks
• Beweis des Satzes von Pythagoras
• Berechnung von  π 

• Flächeninhalt des regelmäßigen Zwölfecks   (1. Buch)

Auf der rechten Briefmarke sieht man die Skizze eines regelmäßigen Zwölfecks mit Umkreis und umbeschriebenem Quadrat. Liu Huis Originalzeichnung ist verschollen; das Bild auf der Briefmarke ist eine spätere Rekonstruktion. Was will Liu Hui beweisen? Er will auf geometrisch-anschaulichem Weg zeigen, dass der Flächeninhalt eines regelmäßigen Zwölfecks  3/4  des Flächeninhalts des umbeschriebenen Quadrats beträgt. Anders ausgedrückt:

Das in ein Quadrat der Seitenlänge  2r  einbeschriebene Zwölfeck hat den Flächeninhalt  3 r².

"Einbeschrieben" bedeutet hier, dass vier Ecken des Zwölfecks (nicht etwa vier Seiten) das Quadrat berühren.

Links in Bild 1 ist diejenige Fläche gelb eingefärbt, deren Flächeninhalt gleich dem eines Quadranten des Quadrates sein soll. Dies beweist man, indem man das linke gelbe Dreieck als flächengleich mit der weißen Fläche im oberen rechten Quadranten nachweist.

1. Schritt : Das orangene Dreieck in der rechten Skizze von Bild 1 ist kongruent zum orangenen Dreieck in der mittleren Skizze rechts oben. In der rechten Skizze ist eine Seite des regelmäßigen Sechsecks eingefügt, mit der Länge  r . Die beiden Dreiecke haben also beide die Basislänge  r . Eine weitere Seite ist ebenfalls gleich, nämlich eine Zwölfeckseite. Der von dieser Seite und der Basis eingeschlossene Winkel ist rechts  15° , weil der Innenwinkel im Zwölfeck  150°  beträgt; der entsprechende Winkel in der mittleren Skizze (also beim Mittelpunkt der oberen Quadratseite) ist ein rechter Winkel abzüglich eines halben Zwölfeck-Innenwinkels, also ebenfalls  15°. Damit ist die Kongruenz nachgewiesen, insbesondere ist das orangene Dreieck in der mittleren Skizze oben rechts gleichschenklig.


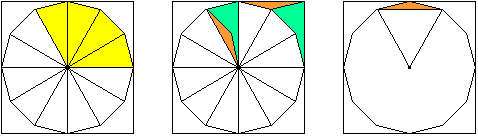
Bild 1

2. Schritt : Überträgt man wie in der mittleren Skizze von Bild 1 das obere orangene Dreieck in einen Zwölfecksektor, so sind die beiden grünen "Rest-"Vierecke kongruent. In Bild 2 sind dies die Vierecke  ABCO  und  DEFG . Zunächst zu den Seiten:  OA = GD = r ; AB = DE  und  BC = EF  und  CO = FG , diese sechs Seiten haben alle die Länge einer Zwölfeckseite, siehe 1. Schritt. Außerdem stimmen die Winkel bei  C  und bei  F  überein ( 360° - Innenwinkel Zwölfeck nach 1. Schritt), sowie die Winkel bei  A  und  D  (jeweils  75° nach 1. Schritt).


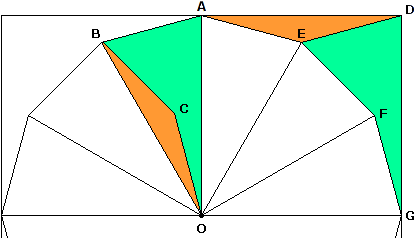
Bild 2

Da eine grüne und eine orangene Fläche zusammen einen Zwölfecksektor bilden, ist der Beweis vollständig.

Liu Hui verwendet dieses Ergebnis noch in einem anderen Zusammenhang. In den "Neun Büchern" wird eine Näherungsformel für Kreissegmente (Kreisabschnitte) angegeben:

Segmentfläche  =  Höhe · ( Höhe + Sehne ) / 2    (näherungsweise)

Die rechte Seite dieser Gleichung ist die Fläche eines Trapezes mit der Sehne als Basis und der gleichen Höhe wie das Segment; die Parallelseitenlänge des Trapezes ist gleich der Höhe (siehe Bild 3).


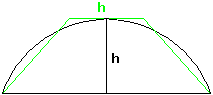
Bild 3

Liu Hui weist nun darauf hin, dass diese "Trapezregel" in guter Näherung gilt, wenn das Segment ein Halbkreis ist, aber für kleinere Segmente (also kleinere Höhen  h ) ungenauer wird. Was meint er mit "guter Näherung"? Das Trapez für den Halbkreis ist in Bild 3a dargestellt. Sein Flächeninhalt ist  h·(s + h)/2 , wegen  s/2 = h = r  also  (3/2)·r² . Dies ist aber gerade der halbe Flächeninhalt des in den Kreis einbeschriebenen regelmäßigen Zwölfecks. Also meint Liu: Das Trapez nähert flächenmäßig den Halbkreis so gut an wie das Zwölfeck den Kreis (dies entspricht der Näherung  3  für  π ).


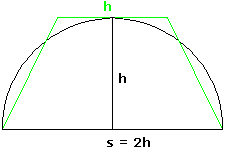
Bild 3a

Gleichzeitig mit dieser Briefmarkenseite erscheint ein mathematisches Problem, in dem Liu Huis Aussage zur Approximationsgüte bei kleineren Höhen untersucht wird.

• Beweis des Satzes von Pythagoras   (9. Buch)

Liu Hui benutzt den Satz von Pythagoras für die Berechnung von  π , die auf der Briefmarke vermerkt ist. Die chinesische Bezeichnung für diesen Satz ist Gou-Gu-Regel; dabei steht Gou für die kürzere und Gu für die längere Kathete. Die Hypotenuse heißt Xian. Lius Beweis besteht aus einer Skizze, die verschollen ist, und aus einem Text, der zunächst zitiert werden soll:

Das Quadrat über Gou sei rot, das Quadrat über Gu sei blau. Die fehlenden und die überschüssigen Teile werden gegenseitig in die entsprechenden Positionen verschoben; die anderen Teile bleiben unverändert. Die Teile ergeben zusammengesetzt das Quadrat über Xian.

Das ist der gesamte Beweis! Ohne die Skizze ist er nicht verständlich. Offenbar führt Liu Hui einen rein geometrischen Beweis ohne jegliche Rechnungen, indem er Teile der Quadrate über den Katheten verschiebt. Lius Landsmann Li Huang hat im 18. Jahrhundert Liu Huis Skizze zur Gou-Gu-Regel rekonstruiert. Man sieht sie links in Bild 4, wobei zunächst die Einfärbung wie in Lius Text fortgelassen wurde; das rechtwinklige Dreieck ist fett gezeichnet. Diese Skizze ist bemerkenswert, denn das kleinere Kathetenquadrat und das Hypotenusenquadrat liegen nicht außerhalb des Dreiecks, wie in den meisten Darstellungen des Pythagoras-Satzes, sondern sind "nach innen", also über das Dreieck hinweg geklappt.


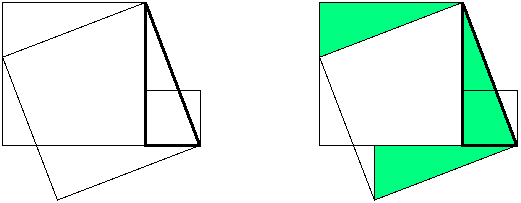
Bild 4

Das Ursprungsdreieck taucht in Li Huangs Skizze insgesamt dreimal auf (grün in Bild 4 rechts). Dies ist eines der Ergebnisse aus der Analyse, die nun von Bild 4 erfolgen soll.

Warum liegt im Bild 4 die linke obere Ecke des Hypotenusenquadrats auf der linken Seite des größeren Kathetenquadrats? Wir lassen zunächst das größere Kathetenquadrat weg und fügen dann wie im folgenden Bild 5 die Dreiecke  A  und  B  an das Hypotenusenquadrat an. Die rechte Skizze in Bild 5 zeigt, dass durch Anfügung von  A  und  B  ein Quadrat der Seitenlänge  a  entsteht (beachte  α + β = 90° ) :


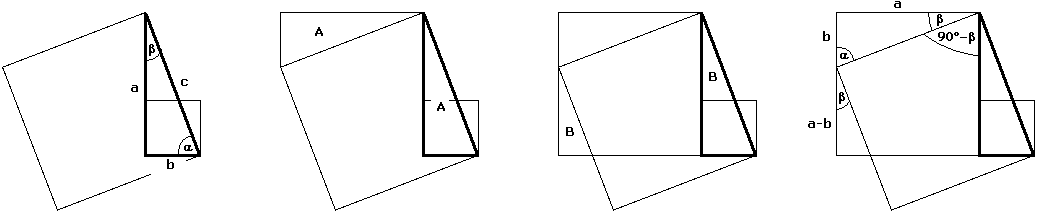
Bild 5

Im folgenden Bild 6 sind die beiden Dreiecke  A  und die beiden Dreiecke  C  jeweils kongruent. Für  A  liegt die Seitenlänge  c  vor, somit für  C  die Seitenlänge  b ; für beide Kongruenzen wurde  β = 90° - α  benutzt.


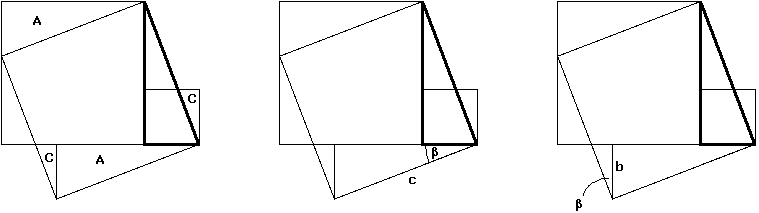
Bild 6  (Mitte: Kongruenz für  A ; rechts: Kongruenz für  C )

Nach diesen Vorbereitungen können wir den Beweis von Liu Hui nachvollziehen:


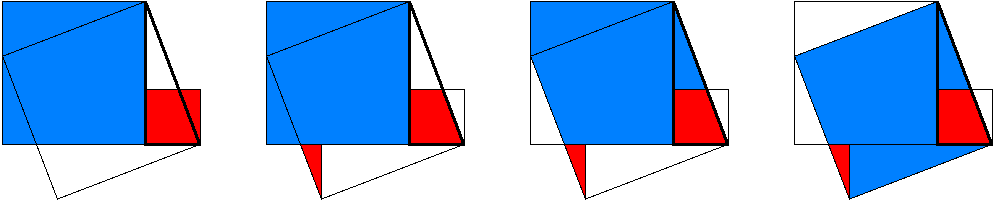
Bild 7

Jetzt wird Lius Beweistext klar. Wir wollen ihn nochmal zitieren:
Das Quadrat über Gou sei rot, das Quadrat über Gu sei blau. Die fehlenden und die überschüssigen Teile werden gegenseitig in die entsprechenden Positionen verschoben; die anderen Teile bleiben unverändert. Die Teile ergeben zusammengesetzt das Quadrat über Xian.
Die "überschüssigen" Teile sind also die drei farbigen Dreiecke, die außerhalb des Hypotenusenquadrats liegen. Die "fehlenden" Teile sind die zunächst weißen Flächen im Hypotenusenquadrat (Bild 7 links). Die für die drei Verschiebungen in Bild 7 notwendigen Kongruenzen haben wir oben nachgewiesen.

• Berechnung von  π    (1. Buch)

Liu Hui gehörte zu den Weltrekordhaltern in der Berechnung von  π . Wie Archimedes approximierte er die Kreisfläche durch regelmäßige  n-Ecke. Er begann mit  n = 6  und verdoppelte dann schrittweise die Seitenzahl, betrachtete also  n = 3·2^k . Seine Berechnungen erstreckten sich auf  k = 1,...,10 . Mit  k = 10  war er beim  3072-Eck angelangt.

Liu Hui untersuchte nur einbeschriebene  n-Ecke und keine umbeschriebenen. Die Fläche der einbeschriebenen  n-Ecke war also jeweils nur eine untere Abschätzung der Kreisfläche. Wir werden aber noch sehen, dass Liu Hui ein eigenes Verfahren zur Abschätzung nach oben anwandte. Die Verwendung von sowohl ein- als auch umbeschriebenen  n-Ecken kann man auf der Tsu Ch'ung Chi gewidmeten Briefmarkenseite als Verfahren des Archimedes nachlesen.  -  Zunächst wollen wir das Arsenal von Methoden angeben, das Liu benutzt hat, wobei immer von einem Kreis mit Radius  1  (also mit Flächeninhalt  π ) ausgegangen wird.

a_n :  Seitenlänge des einbeschriebenen regelmäßigen  n-Ecks

A_n :  Flächeninhalt des einbeschriebenen regelmäßigen  n-Ecks

c_n :  Abstand Seitenmitte - Kreisrand

d_n :  Abstand Seitenmitte - Kreismitte      ( c_n + d_n = 1 )



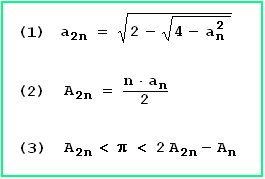
(1) - (3) sollen nun bewiesen werden; siehe dazu Bild 8. Es wird der Satz des Pythagoras (Gou-Gu-Regel) verwendet, den Liu Hui selbst bewiesen hat (s.o.).


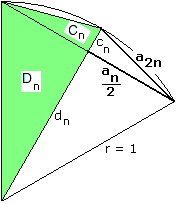
Bild 8


Beweis von  ( 1 ) :




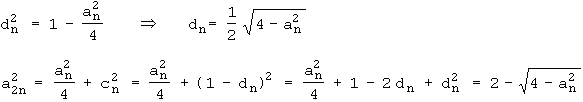
Beweis von  ( 2 ) :




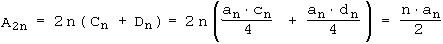
Beweis von  ( 3 ) :




Mit Hilfe dieser Formeln gelangt Liu Hui zunächst zu einem ersten Ergebnis, indem er bis  k = 5  vorschreitet und alle auftretenden Wurzeln möglichst genau durch Brüche nähert. Seine letzten Schritte dabei sind:



Es folgt mit (3):



Für dieses Ergebnis kann man in Lius Buch alle Einzelschritte rechnerisch konkret nachlesen. In der Literatur (z.B. [2]) wird aber Liu Hui ein noch wesentlich präziserer Näherungswert für  π  zugeschrieben, nämlich:



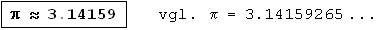
In Lius Buch findet man explizit nur die Näherung  3.1416  (was auch schon ein sehr guter Wert ist), aber er schreibt selbst, dass er dieses Resultat durch die Berechnung von  A₃₀₇₂  mittels (1) und (2) erhalten hat. In [1] wird dafür als Zwischenwert näherungsweise  a₁₅₃₆ = 0.0040906  angegeben, aber dies ist ein abgerundetes Ergebnis, mit dem man nicht auf die Genauigkeit von fünf Nachkommastellen für  π  kommen kann. Rechnet man dagegen mit Lius Wert  0.065438  für  a₉₆  (s.o.) weiter bis  a₁₅₃₆  und wendet dann (3) an, so erhält man  3.1415825 < π < 3.1415891 . Dass die rechte Ungleichung nicht stimmt, liegt an der Fehlerfortpflanzung von  a₉₆ , denn schon hier ist Lius Wert etwas zu klein. Letzte Zweifel daran, wie genau Liu Hui  π  berechnet hat  -  auf vier oder auf fünf Nachkommastellen  - , lassen sich also nicht ganz ausräumen.




Literatur

[1] Shen Kangshen, John N. Crossley, Anthony W.-C. Lun: The Nine Chapters on the Mathematical Art  -  Companion and Commentary, Oxford 1999
[2] Johann Wiesenbauer: Algorithmen zur numerischen Berechnung von  π ; in: Didaktik der Mathematik, Band 1, Klagenfurt 1976


Kategorie: Chinesische Mathematik

Kategorie: Zahlen und Zahlsysteme, Berechnung von π

Publiziert 2006-11-13          Stand 2006-04-15