
Michel 785
Scott 832
| Manfred Börgens Mathematik auf Briefmarken # 55 |
Liste aller Briefmarken vorige Marke nächste Marke |
zur Leitseite |
 |
Sri Lanka 1987 Michel 785 Scott 832 |
Kuboktaeder - ein Archimedischer Körper
Zum Vollmond am 13. Mai :
Das Vesak-Fest im buddhistischen Jahr 2531
Vesak ist das wichtigste Fest der Buddhisten. Es wird vielerorts am ersten Vollmondtag im Mai gefeiert, aber es gibt regionale Abweichungen. Die Briefmarke wurde zum Vesak-Fest des Jahres 1987 herausgegeben, dem das Jahr 2531 nach buddhistischer Zählung entspricht, wie auf der Marke zu sehen ist. 1987 fiel der Mai-Vollmond auf den 13.5., wie auch in diesem Jahr (2006). Vesak erinnert an das "Erwachen" oder die "Erleuchtung" Buddhas. In manchen Ländern, auch in Sri Lanka, wird das Fest mit Lichterprozessionen begangen. Auf der Briefmarke sieht man deshalb Laternen. Die Gestalt der beim Vesak getragenen Laternen ist vielfältig und einfallsreich; die hier abgebildeten haben die Form von Kuboktaedern, also von Polyedern mit sechs Quadraten und acht gleichseitigen Dreiecken als Seitenflächen. In jeder der zwölf Ecken stoßen zwei Quadrate und zwei Dreiecke zusammen, an jeder der 24 Kanten treffen sich ein Quadrat und ein Dreieck. Auf diese Weise entsteht ein schöner Körper von hoher Symmetrie, der sich zudem leicht aus Papier zu einer Laterne falten lässt. Bild 1 zeigt, wie man ein Kuboktaeder herstellen kann.
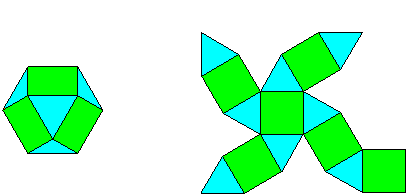
Bild 1 Kuboktaeder mit ebenem Netz
Die Erklärung auf der Briefmarke "OCTAGONAL LANTERNS" ist nicht nachzuvollziehen. Ein Oktagon ist ein Achteck und hat keinen erkennbaren Bezug zum Kuboktaeder.
Die Archimedischen Körper
Die Archimedischen Körper sind eine Unterklasse der konvexen Polyeder. Schon in der Antike wurden die fünf Platonischen Körper untersucht, konvexe Polyeder, deren Flächen kongruente regelmäßige Polygone sind (dass diese Beschreibung alleine nicht ausreicht, kann man im Problem # 29 nachlesen). Bei den Archimedischen Körpern entfällt die Forderung nach der Kongruenz; hier sind die Flächen regelmäßige Polygone verschiedenen Typs, d.h. nicht alle Flächen haben die gleiche Eckenzahl (aber natürlich gleiche Kantenlängen). Außerdem wird eine weitgehende Symmetrieeigenschaft verlangt: Jede Ecke kann durch eine Symmetrieoperation auf eine beliebige andere Ecke abgebildet werden (Symmetrieoperationen sind Drehungen, Spiegelungen oder Kombinationen davon, die das Polyeder unverändert lassen). Schließlich ordnet man den uniformen Prismen und Antiprismen eine eigene Unterklasse der konvexen Polyeder zu. Dann bleiben genau 13 Polyeder übrig, nämlich die Archimedischen Körper. Zusammen mit den Platonischen Körpern sowie den Prismen und Antiprismen bilden die Archimedischen Körper die Klasse der konvexen uniformen Polyeder.
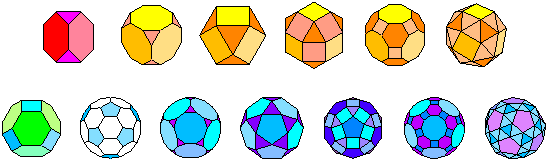
Bild 2 Archimedische Körper
In Bild 2 erkennt man gut die Symmetrieeigenschaften der Archimedischen Körper. Man sieht, dass zehn dieser Körper zwei Polygontypen und drei Körper drei Polygontypen als Flächen aufweisen; mehr als drei Typen können nicht vorkommen. Es gibt als Flächen 3-, 4-, 5-, 6-, 8- und 10-Ecke. Alle Ecken eines Archimedischen Körpers liegen auf einer Kugel. - Das Kuboktaeder gehört offensichtlich zu den einfacheren Archimedischen Körpern.
Die Arbeit von Archimedes über die nach ihm benannten Körper ist verschollen. Etliche dieser Körper waren aber schon vor ihm bekannt. Andere Leistungen von Archimedes wurden bei der Briefmarke # 33 kommentiert. Nach Archimedes war Johannes Kepler der erste, der eine komplette und bebilderte Liste der 13 Körper aufstellte.
Das Kuboktaeder
Ein Kuboktaeder lässt sich aus den Platonischen Körpern Würfel und Oktaeder durch Kappung der Ecken herstellen. Man schneidet alle Ecken ab, mit Schnittebenen jeweils durch die nächstliegenden Kantenmitten. Beim Würfel werden aus den ursprünglichen sechs quadratischen Flächen auf diese Weise sechs neue Quadrate mit halbem Flächeninhalt; durch die Eckenkappung entstehen die acht Dreieckflächen des Kuboktaeders. Beim Oktaeder werden aus den ursprünglichen acht Dreiecken jeweils neue Dreiecke mit gevierteltem Flächeninhalt; durch die Eckenkappung entstehen die sechs Quadratflächen des Kuboktaeders. Im linken Feld von Bild 3 kann man den Kappungsprozess verfolgen: Kappt man die Würfelecken, so bleiben die roten Flächen stehen und die gelben Flächen sind die Schnittflächen; fängt man rechts an und kappt man die Oktaederecken, so bleiben die gelben Flächen stehen und die roten sind die Schnittflächen. Im rechten Feld von Bild 3 ist dieser Prozess integriert dargestellt: Man sieht dort Würfel und Oktaeder so überlagert, dass die Kantenmitten zusammenfallen; schneidet man jetzt alle Ecken (grüne und violette) weg, erhält man ein Kuboktaeder.
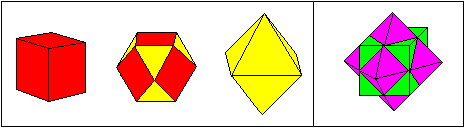
Bild 3 Kuboktaeder als Restkörper
Das Kuboktaeder besitzt eine bemerkenswerte Symmetrieeigenschaft: Das Netz der 24 Kanten besteht aus vier regulären Sechsecken, die jeweils den Körper in zwei identische Hälften teilen. Dies ist in Bild 4 dargestellt.
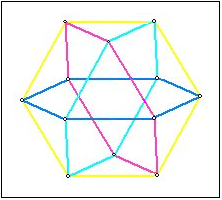
Bild 4 Kantennetz Kuboktaeder
Das Kuboktaeder kommt in der Natur vor. Die Mineralien Flussspat (Fluorit, CaF2), Silberglanz (Argentit, Ag2S) und Bleiglanz (Galenit, PbS) kristallisieren als Kuboktaeder (aber auch in anderen Formen).
Mein Kuboktaeder aus Stein
Polyeder-Kupferstiche von Wenzel Jamnitzer
Publiziert 2006-04-23 Stand 2009-01-25