Dodekaeder    MB Matheblog # 32 Inhalt Blog
voriger Eintrag    nächster Eintrag		 zur Leitseite
Index der gesamten Website


2024-02-26


Ein geometrisches Problem, dessen Lösung 3× L'Hospital in Folge erfordert


Dieser Beitrag greift das Problem # 57 auf dieser Website auf, aus dem ein bemerkenswertes Detail hervorgehoben und genauer dargestellt werden soll. Auf der Briefmarke # 57 ist der chinesische Mathematiker Liu Hui abgebildet, auf den dieses geometrische Problem zurückgeht.

Es wird gezeigt, dass die Aufgabenstellung von Liu Hui auf ein Grenzwertproblem führt, das die sukzessive dreifache Anwendung des Satzes von L'Hospital erforderlich macht.

Der Satz von L'Hospital (der eigentlich nicht dem Marquis de L'Hospital, sondern Johann Bernoulli zuzuschreiben ist), enthält als wichtigen Unterfall \[\lim \limits_{x \to a}~\frac{f(x)}{g(x)} = \lim \limits_{x \to a}~\frac{f~'~(x)}{g~'~(x)}~,~~{\small \text{falls der rechte Grenzwert ex. und}}~~\lim \limits_{x \to a}~f(x) = \lim \limits_{x \to a}~g(x) = 0\] und lässt sich wiederholt anwenden, wenn die Ableitungen ebenfalls den Grenzwert \(~0~\) haben.

Beispiele für die wiederholte Anwendung des Satzes lassen sich leicht generieren, aber bei realen  –  also nicht zu Übungszwecken erfundenen  –  Problemen trifft man das nur vereinzelt an. Das geometrische Problem von Liu Hui führt nun sogar bis zu den 3. Ableitungen von Zähler und Nenner.

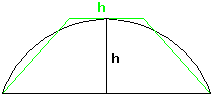
Wir wollen den von Liu Hui gewählten Ansatz die Chinesische Trapezregel nennen. Mit dieser wurde der Flächeninhalt eines Kreissegments näherungsweise durch die Fläche eines Trapezes berechnet, das in der Höhe mit dem Segment übereinstimmt und dessen parallele Seiten die Längen von Segmentsehne und Höhe haben, siehe Bild 1.

Trapezregel

Bild 1   Chinesische Trapezregel

Diese Approximation ist recht ungenau. Um das zu zeigen, nehmen wir o.E. den Kreisradius 1 und bedienen uns des halben Mittelpunktwinkels für das Segment, siehe Bild 2.

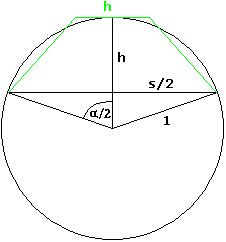
Trapezregel mit Winkel

Bild 2   Chinesische Trapezregel mit halbem Mittelpunktwinkel

Damit erhalten wir die folgenden Beziehungen: \[\text{cos}~\frac{\alpha}{2} = 1-h~~~~~~~~~~\text{sin}~\frac{\alpha}{2} = \frac{s}{2}\] Die Flächeninhalte sind (siehe Problem # 57): \[{\small \text{Trapez}}~~~~h\cdot\frac{h+s}{2}~~~~~~~~~~{\small \text{Segment}}~~~~\frac{1}{2}(\alpha - \text{sin}~\alpha)\] und somit \[{\small \text{Trapez}}~~~~\frac{1}{2}~\left(1-\text{cos}~\frac{\alpha}{2}\right)~\left(1-\text{cos}~\frac{\alpha}{2}+2~\text{sin}~\frac{\alpha}{2}\right)~~~~~~~~~~{\small \text{Segment}}~~~~\frac{\alpha}{2} - \text{sin}~\frac{\alpha}{2}~\text{cos}~\frac{\alpha}{2}\] Mit \(~x = \alpha/2~\) ist dann das Verhältnis von Trapez- zu Segmentfläche

\[y(x) = \frac{(1-\text{cos}~x)(1-\text{cos}~x+2~\text{sin}~x)}{2x-2~\text{sin}~x~\text{cos}~x} =\frac{f(x)}{g(x)}~~~~~~~~~x~\in\left(0,\frac{\pi}{2}\right]\]


Für \(~x = \pi/2~\) ist das Segment ein Halbkreis mit \(~y(\pi/2) = 3/\pi \approx 0,955~\)  –  das ist eine recht gute Näherung. In Problem # 57 wurde gezeigt, dass \(~y~\) streng monoton wächst; der Graph ist in Bild 3 zu sehen.


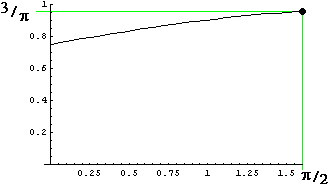
Graph y

Bild 3   Verhältnis von Trapez- zu Segmentfläche als Funktion des halben Mittelpunktwinkels


Der andere Grenzwert für \(~x \rightarrow 0~\) macht mehr Mühe. \[\lim \limits_{x \to 0}~f(x) = \lim \limits_{x \to 0}~g(x) = 0\] Wir wenden den Satz von L'Hospital an. \[\lim \limits_{x \to 0}~f~'~(x) = \lim \limits_{x \to 0}~(-2 + 2~\text{sin}~x + 2~\text{cos}~x + 4~\text{sin}^2~x - 2~\text{sin}~x~\text{cos}~x) = 0\] \[\lim \limits_{x \to 0}~g~'~(x) = \lim \limits_{x \to 0}~4~\text{sin}^2~x = 0\] Und nochmal: \[\lim \limits_{x \to 0}~f~''~(x) = \lim \limits_{x \to 0}~(-2 - 2~\text{sin}~x + 2~\text{cos}~x + 4~\text{sin}^2~x + 8~\text{sin}~x~\text{cos}~x) = 0\] \[\lim \limits_{x \to 0}~g~''~(x) = \lim \limits_{x \to 0}~8~\text{sin}~x~\text{cos}~x = 0\] Und noch einmal: \[\lim \limits_{x \to 0}~f~'''~(x) = \lim \limits_{x \to 0}~(8 - 2~\text{sin}~x - 2~\text{cos}~x - 16~\text{sin}^2~x + 8~\text{sin}~x~\text{cos}~x) = 6\] \[\lim \limits_{x \to 0}~g~'''~(x) = \lim \limits_{x \to 0}~(8 - 16~\text{sin}^2~x) = 8\] Wie oben angekündigt: Erst die dritte Anwendung des Satzes von L'Hospital liefert das Ergebnis.

\[\lim \limits_{x \to 0}~y(x) = \lim \limits_{x \to 0}~\frac{f~'''~(x)}{g~'''~(x)} = \frac{3}{4}\]

Dieser Grenzwert harmoniert mit dem Graphen in Bild 3. Er zeigt auch, dass die Approximation von Liu Hui für kleine Segmente ungeeignet ist.



Kategorie: Chinesische Mathematik


Stand 2022-01-11

Inhalt Blog   |    voriger Eintrag   |    nächster Eintrag

Manfred Börgens   |   Zur Leitseite