Problem des Monats Februar 2004

A. mischt die Skatkarten und sagt zu B. und C.: "Einer von Euch könnte doch mal Bier holen gehen." B. und C. werden sich nicht einig, wer gehen soll. A. schlägt vor: "Ich lege zwei Karten nebeneinander auf den Tisch, die ich zufällig gezogen habe. Wenn sie beide von der gleichen Farbe - schwarz oder rot - sind, geht B., bei verschiedenfarbigen Karten geht C."

B. und C. sind einverstanden und C. wird auf diese Weise als Bierholer ausgelost. Auf dem Weg zur Theke kommen ihm Zweifel, ob A.'s Vorschlag wirklich fair war.

C.'s Zweifel sind berechtigt. Warum?

Kann man das "Ausloseverfahren" von A. nur mit einem (evtl. kleinen) Teil der Skatkarten durchführen, so dass B. und C. fair behandelt werden?

Diese Auswahl von Karten ergibt keine faire Auslosung des Bierholers !

Lösung

Ein Kartenspiel mit  r  Karten enthält  n  schwarze und  r - n  rote Karten. Es werden zwei Karten zufällig gezogen. Die erste Karte wird nicht zurückgelegt, bevor die zweite gezogen wird. In der Problemstellung ist zunächst  r = 32  und  n = 16 . Zwei Zahlen sollen verglichen werden:

g = Anzahl möglicher Ziehungen für zwei Karten gleicher Farbe
u = Anzahl möglicher Ziehungen für zwei Karten verschiedener Farbe

Wir wollen annehmen, dass A. die erste Karte links und die zweite Karte rechts hinlegt.

Möglichkeiten für g :
linke Karte schwarz ( n  Mögl.) und rechte Karte schwarz ( n - 1  Mögl.)
oder
linke Karte rot ( r - n  Mögl.) und rechte Karte rot ( r - n - 1  Mögl.)

Möglichkeiten für u :
linke Karte schwarz ( n  Mögl.) und rechte Karte rot ( r - n  Mögl.)
oder
linke Karte rot ( r - n  Mögl.) und rechte Karte schwarz ( n  Mögl.)

So erhält man:

g = n·(n - 1) + (r - n)·(r - n - 1)
u = 2·n·(r - n)

C.'s Bedenken waren berechtigt: Für  r = 32  und  n = 16  erhält man  g = 480  und  u = 512 . Da es insgesamt  r·(r - 1) = 992  mögliche Ziehungen gibt, muss B. mit Wahrscheinlichkeit  480/992 , also ca.  0.484  Bier holen, C. dagegen mit Wahrscheinlichkeit  512/992 , also ca.  0.516 .

B. und C. werden fair behandelt, wenn  g = u  ist. Multipliziert man die Ausdrücke für  g  und  u  aus und setzt sie gleich, erhält man zunächst:

g = u   <-->   r = (2n - r)²

Also muss das Kartenspiel eine quadratische Anzahl von Karten haben, damit das Losverfahren fair ist. Außerdem sieht man: Gleich viele schwarze wie rote Karten führen nie zu einem fairen Verfahren, denn dann wäre  2n = r , also  r = 0.

Gibt es für jede Quadratzahl  r > 1  auch eine Zusammenstellung von schwarzen und roten Karten für ein faires Verfahren? Wir müssen zwei Fälle unterscheiden. Ist  2n < r , so löst man die Gleichung  r = (2n - r)²  zu  n = (r - r^1/2)/2  auf  (dann ist  r - n = (r + r^1/2)/2 ) , ansonsten zu  n = (r + r^1/2)/2  (mit  r - n = (r - r^1/2)/2 ) .  n  und  r - n  sind dann jeweils natürliche Zahlen, denn  r  und  r^1/2  sind entweder beide gerade oder beide ungerade. Zusammengefasst heißt das:

Für ein faires Losverfahren muss das Kartenspiel  (r - r^1/2)/2  schwarze und  (r + r^1/2)/2  rote Karten enthalten oder umgekehrt.  r  ist dabei eine beliebige Quadratzahl  > 1.

Setzt man  r = m² , so erkennt man, dass die Anzahlen für schwarze bzw. rote Karten  m·(m - 1)/2  und  m·(m + 1)/2  aufeinanderfolgende Dreieckszahlen sind.

Also gibt es im wesentlichen für A. nur vier Möglichkeiten, schwarze und rote Karten aus einem Skatspiel so zusammenzustellen, dass die Chancen für B. und C. gleich sind:

 1  -   3
 3  -   6
 6  -  10
10  -  15

Abschließende Bemerkung:
Dass die Summe eines Paars von Dreieckszahlen eine Quadratzahl ist, lässt sich grafisch veranschaulichen ("Beweis ohne Worte"):




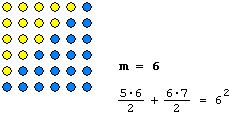
Kategorie: Beweise ohne Worte