Das Nur-Dach-Haus

          Die Lösung steht im unteren Teil der Seite.

Unser "Nur-Dach-Haus" hat im Wesentlichen eine normale Hausform, aber die beiden Dachflächen sind bis auf den Boden heruntergezogen. Deshalb gibt es außen keine Seitenwände, aber zwei dreieckige Giebel. Dies sieht man in Bild 1. Dort erkennt man auch, dass der eigentliche Wohnbereich aus einem Quader besteht; außerdem gibt es einen Dachboden (Spitzboden) über dem Quader und zwei abgeschrägte Lagerräume links und rechts vom Quader.

Ganz perfekte Nur-Dach-Häuser bestehen nur aus dem Dach und zwei Giebeln, haben also keinen Quader im Inneren.


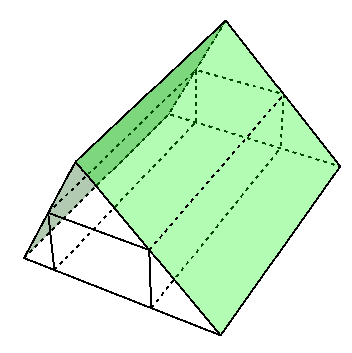
Bild 1

Bei den nun folgenden Optimierungsproblemen spielt die Länge des Dachfirsts (gleich der Länge des Quaders) keine Rolle, sie soll als fest gewählt angenommen werden. Alle weiteren Überlegungen betreffen nur den Querschnitt des Hauses, siehe Bild 2.



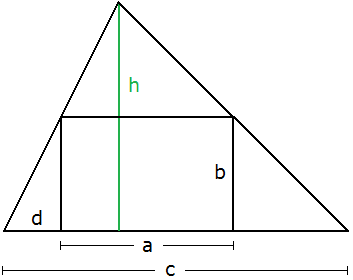
Bild 2

In Bild 2 sind die Maße des Quaders vermerkt: Breite \(~a~\),  Höhe \(~b~\). Diese sollen im Folgenden immer als fest gewählt angenommen werden. Variabel sind dagegen die Basisbreite \(~c~\) des Hauses, die Haushöhe \(~h~\) und der Abstand \(~d~\) der linken unteren Quaderkante vom linken Fußpunkt des Dachs.

Mit "Giebel" ist im Folgenden das große Dreieck mit Basis \(~c~\) und Höhe \(~h~\) gemeint.

Bei festem \(~c~\) ist der Quader auf der Hausbasis verschieblich, indem \(~d~\) variiert wird; dann verändern sich auch die Neigungen der beiden Dachflächen, also im Querschnitt die Winkel des Giebels.

Aufgabe 1
Wie hängen \(~h~\) (und damit die Giebelfläche) und die Dachfläche bei  festem \(~\textbf{c}~\) von \(~d~\) ab? Insbesondere sollen Grenzwerte und Extrema berechnet werden.

Aufgabe 2
Nun soll \(~\textbf{c}~\) variabel sein. Wie hängen \(~h~\),  die Giebelfläche und die Dachfläche von \(~c~\) ab? Insbesondere sollen Grenzwerte und Extrema berechnet werden. Dabei ergibt sich die Wahl von \(~d~\) aus Aufgabe 1.

Lösung

Aufgabe 1

Das Dreieck des Dachbodens ist ähnlich zum großen Giebeldreieck (siehe Bild 2), und zwar im Verhältnis \(~a:c~\) für die Seiten und Höhen. Damit erhält man für die Höhe \(~h~\) und die Giebelfläche \(~A~\): \[h~=~b+\frac{h\cdot a}{c}~~~~\Rightarrow~~~~h=\frac{b\cdot c}{c-a}\] \[A=\frac{c\cdot h}{2}=\frac{b\cdot c^2}{2(c-a)}\] \(h~\) und \(~A~\) hängen nicht von \(~d~\) ab. Man kann also bei festem \(~c~\) das Rechteck beliebig auf der Dreiecksbasis verschieben, ohne die Höhe und die Fläche des Dreiecks zu verändern.

Wegen der festen Firstlänge ist für die Dachfläche nur die Länge der Dachkante relevant, also \(~s_1+s_2~\) in Bild 3.



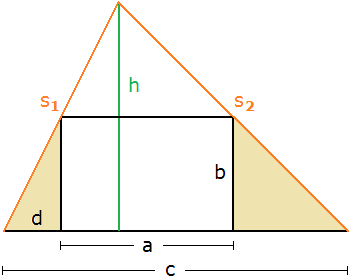
Bild 3

Wir verwenden wieder das Ähnlichkeitsargument (wie oben für \(~h~\)) : \[s_1=\sqrt{b^2+d^2~}~+\frac{s_1 \cdot a}{c}~~~\Rightarrow~~~s_1=\frac{c}{c-a}\cdot \sqrt{b^2+d^2~}\] \[s_2=\sqrt{b^2+(c-a-d)^2~}~+\frac{s_2 \cdot a}{c}~~~\Rightarrow~~~s_2=\frac{c}{c-a}\cdot \sqrt{b^2+(c-a-d)^2~}\] \[\lim_{d~\to~0} (s_1+s_2)=\lim_{d~\to~c-a} (s_1+s_2)=\frac{c}{c-a}\cdot \left(b+\sqrt{b^2+(c-a)^2~}\right)\] Ableiten von \(~s=s_1+s_2~\) nach \(~d~\) und Extremumsuche: \[s^{'}=\frac{c}{c-a} \cdot \left(\frac{d}{\sqrt{b^2+d^2~}}-\frac{c-a-d}{\sqrt{b^2+(c-a-d)^2~}}\right)~\mathop{=}_\lt^{\gt}~0~~~~~\Leftrightarrow\] \[~~~~~\Leftrightarrow~~~~~d^2 \cdot (b^2+(c-a-d)^2)~\mathop{=}_\lt^{\gt}~(c-a-d)^2 \cdot (b^2+d^2)~~~~~~\Leftrightarrow~~~d~\mathop{=}_\lt^{\gt}~\frac{c-a}{2}\] Also hat die Dachfläche ein absolutes und striktes Minimum für \(~d=\frac{c-a}{2}~\).  Dann ist der Giebel symmetrisch mit \(~s_1=s_2~\).  Für die minimale Länge der Dachkante gilt: \[\textbf{(1)}~~~~d=\frac{c-a}{2}~~~\rightarrow~~~s_{min}=\frac{c}{c-a}\cdot \sqrt{4b^2+(c-a)^2}\]

Aufgabe 2 \[c\in(a,+\infty)\] \[\lim_{c~\to~a} h=+\infty~~~~~\lim_{c~\to~\infty} h=b\] \(h~\) fällt streng monoton mit \(~c~\) und hat kein Extremum. Die Wahl von \(~d~\) hat keine Wirkung auf \(~h~\) (Aufgabe 1).

\[\lim_{c~\to~a} A=+\infty~~~~~\lim_{c~\to~\infty} A=+\infty\] Ableiten nach \(~c~\) und Extremumsuche: \[A^{'}=\frac{b}{2} \cdot \frac{2c\cdot (c-a)-c^2}{(c-a)^2}=\frac{bc}{2} \cdot \frac{c-2a}{(c-a)^2}~\mathop{=}_\lt^{\gt}~0~~~~\Rightarrow~~~~c~\mathop{=}_\lt^{\gt}~2a\] \(A~\) hat also genau ein Extremum, und zwar ein striktes und absolutes Minimum (das nicht von \(~b~\) abhängt) für \(~c=2a~\). Die Wahl von \(~d~\) hat keine Wirkung auf \(~A~\) (Aufgabe 1). \[\textbf{(2)}~~~~c=2a~~~\rightarrow~~~A_{min}=2ab\]

Nun zu \(~s~\).  Für \(~c\rightarrow a~\) gilt \(~d\rightarrow 0~\), also gilt nach Aufgabe 1: \[\lim_{c~\to~a} s=+\infty\] \(s_1,~s_2~\) und \(~h~\) sind Seiten eines Dreiecks (Bild 3), also gilt \(~s_1+s_2\gt c~\) und somit: \[\lim_{c~\to~\infty} s=+\infty\] Wir suchen also ein Minimum. Für jedes \(~c~\) ist nach (1) \(~d=\frac{c-a}{2}~\) zu wählen (minimale Dachfläche bei symmetrischem Dach): \[s=s_1+s_2=\frac{c}{c-a}\cdot \sqrt{4b^2+(c-a)^2}\] Für die Extremumsuche ist es einfacher, \(~s^2~\) zu betrachten: \[s^2=c^2+\left(\frac{2bc}{c-a}\right)^2\] \[(s^2)^{'}=2c+\frac{4bc}{c-a}\cdot \frac{-2ab}{(c-a)^2}=2c~\left(1-\frac{4ab^2}{(c-a)^3}\right)~\mathop{=}_\lt^{\gt}~0~~~~~\Leftrightarrow~~~~~(c-a)^3~\mathop{=}_\lt^{\gt}~4ab^2~~~~~\Leftrightarrow~~~~~c~\mathop{=}_\lt^{\gt}~a+\sqrt[\scriptstyle 3]{4ab^2}\] Wir haben also genau ein Extremum für \(s~\) gefunden, und zwar ein striktes und absolutes Minimum: \[\textbf{(3)}~~~~c=a+\sqrt[\scriptstyle 3]{4ab^2}~~~\rightarrow~~~s_{min}=a\cdot\left(1+\left(\frac{2b}{a}\right)^{2/3}\right)^{3/2}\]

Publiziert 2023-06-18          Stand 2021-01-06

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem