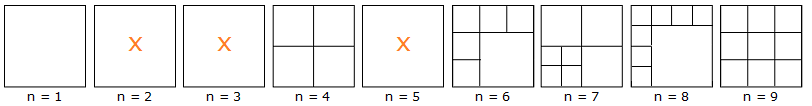Teilung des Quadrates in Quadrate
Die Lösung steht im unteren Teil der Seite.
Wir wollen ein Quadrat in n Teilquadrate zerlegen. Das ist offenbar ganz einfach, wenn n eine Quadratzahl ist, siehe Bild 1 für n = 1, n = 4 und n = 9 . Das Bild zeigt auch, dass es andere, wesentlich unregelmäßigere Lösungen gibt, hier für n = 14 .

Bild 1
Eine Hauptaufgabe wird also sein, diejenigen n zu bestimmen, für die eine Zerlegung möglich ist.

Bild 2
Wir wollen in mehreren Einzelschritten vorgehen. Falls es nötig wird, einzelne Seitenlängen der Teilquadrate anzugeben, soll o.E. die Seitenlänge des Ursprungsquadrates (n = 1) als 1 gesetzt werden. Die Menge aller Zerlegungen in n Teilquadrate bezeichnen wir mit Qn . Dabei sollen Zerlegungen, die durch Spiegelungen oder Rotationen auseinander hervorgehen, als eine einzige Zerlegung betrachtet werden, d.h. die Elemente von Qn sind Äquivalenzklassen, für die es ausreicht, jeweils einen einzigen Vertreter graphisch darzustellen.
Aufgabe 1
Durch Probieren können Sie ohne größere Mühe die Fälle n = 1, 2, ..., 9 behandeln.
Kleiner Tipp:
Regel A: Für n > 1 müssen die 4 Ecken von Q1 nach der Zerlegung in Qn von 4 disjunkten Quadraten besetzt sein.
Der Genauigkeit halber sei angemerkt, dass hier "disjunkt" für "disjunkt mit Ausnahme der Randpunkte" verwendet wird.
Außerdem ist es hilfreich, sich die minimale oder maximale Anzahl von Teilquadraten zu überlegen, die an eine Seite von Q1 anstoßen. Für n = 7 und n = 8 sollte man sich anschauen, ob die Lösungen für kleinere n verwendet werden können.
Aufgabe 2
Für alle n > 8 kann man versuchen, Q6, Q7 und Q8 weiter zu zerlegen.
Aufgabe 3
Eindeutigkeit und Quasi-Eindeutigkeit : Die Lösung von Aufgabe 2 führt auch noch auf ein weiteres Ergebnis, nämlich auf die unterschiedliche Anzahl der Äquivalenzklassen in Qn . Unter Eindeutigkeit wollen wir hier verstehen, dass Qn aus einer einzigen Äquivalenzklasse besteht, also |Qn| = 1 . Unter Quasi-Eindeutigkeit wollen wir verstehen, dass |Qn| > 1 , aber die verschiedenen Größen der Teilquadrate und deren jeweilige Anzahlen sich in den Äquivalenzklassen nicht unterscheiden. Man kann sich dies wie ein Puzzle aus Quadraten vorstellen, das man auf mindestens zwei nicht-äquivalente Weisen zu einem großen Quadrat zusammensetzen kann, und dass außerdem keine weitere Lösung mit anderen Größen oder Anzahlen der Teilquadrate existiert. Es ist nicht unmittelbar klar, ob Quasi-Eindeutigkeit überhaupt vorkommt.
Für welche n gilt |Qn| ≤ 2 ? Für welche n liegt Quasi-Eindeutigkeit vor ? Bestimmen Sie auch den Umfang der einzelnen Äquivalenzklassen für diese n .
In vereinfachter Form (ohne Eindeutigkeit und Äquivalenzklassen) erschien dieses Problem im Buch A Walk Through Combinatorics von Miklos Bona.
Lösung
Aufgabe 1
n = 1, 2, ..., 9 .
Wegen Regel A sind Q2 und Q3 leere Mengen.
Für Q4 wurde in der Aufgabenstellung schon eine Lösung angegeben. Diese Lösung ergibt sich auch direkt aus Regel A, da verschieden große Teilquadrate zu einer Überlappung führen würden. Bild 3 zeigt diesen Ansatz nicht nur für n = 4 , sondern auch gleich für n = 5 , denn in beiden Fällen liegen an mindestens drei Seiten (im Bild links, unten und rechts) genau zwei Teilquadrate mit den Seitenlängen a und 1-a . Damit sich die Teilquadrate in Bild 3 nicht überlappen, muss a = 0,5 sein. Insbesondere ist Q5 die leere Menge.
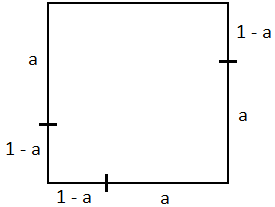
Bild 3
Für n = 6 gibt es (mindestens) zwei Seiten mit genau zwei angrenzenden Teilquadraten. Diese Seiten können nicht einander gegenüber liegen. Dies sieht man in der linken Skizze von Bild 4; dort müsste a = b = 0,5 wie in Q4 sein, damit sich die Teilquadrate nicht überlappen - aber von Q4 kommt man nicht nach Q6 , da wir schon gesehen haben, dass sich ein Quadrat nicht in zwei oder drei Teilquadrate zerlegen lässt.
Also erhält man zunächst eine Konstellation wie in der zweiten Skizze von Bild 4. Damit sind drei Teilquadrate vergeben; das größte unten rechts muss eine Seitenlänge a ≥ 0,5 haben, damit sich die anderen beiden nicht überlappen. a = 0,5 ist nicht möglich, wie wir schon bei der linken Skizze gesehen haben. Die dritte Skizze in Bild 4 zeigt den nächsten Schritt: Es sind noch drei Teilquadrate zu positionieren, oben links mit Seitenlänge 1 - a , die beiden anderen grenzen links und oben an die Seiten des Ursprungsquadrates Q1 an. Offenbar wurde in der Skizze a zu groß gewählt, denn links und oben sieht man Rechtecke, die nicht quadratisch sind. Ihre Seitenlänge entlang von Q1 ist 2a - 1 . Damit dort Quadrate entstehen, muss 2a - 1 = 1 - a , also a = 2/3 sein; dies sieht man in der rechten Skizze von Bild 4 - damit ist Q6 konstruiert. Die Äquivalenzklasse besteht aus 4 Elementen, da das große Quadrat in jeder der 4 Ecken liegen kann.
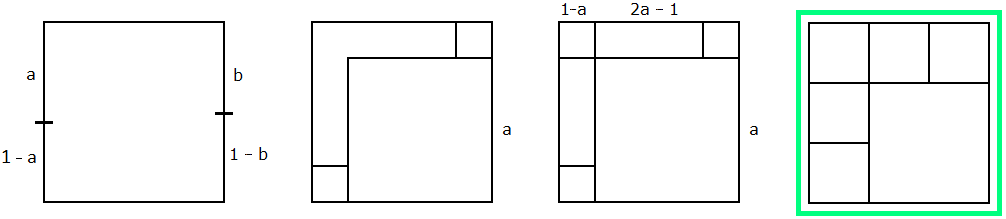
Bild 4 n = 6
Zu n = 7 und n = 8 wurde schon in der Aufgabenstellung ein Tipp gegeben. Q7 erhält man aus Q4 , indem man eines der Teilquadrate viertelt. Die zugehörige Äquivalenzklasse enthält 4 Elemente, da jedes der 4 Teilquadrate in Q4 geviertelt werden kann (siehe Bild 5).
Für Q8 dient Q6 als Vorbild:
Regel B: Für alle geraden n ≥ 4 kann man ein Quadrat der Seitenlänge 1 - 2/n in eine Ecke legen, so dass es an zwei Seiten von einem "Saum" von n - 1 gleich großen Quadraten der Seitenlänge 2/n umgeben wird.
Für n = 8 erhalten wir auf diese Weise Teilquadrate mit den Seitenlängen 3/4 und 1/4 .
Wir ziehen in Bild 5 ein Zwischenfazit:
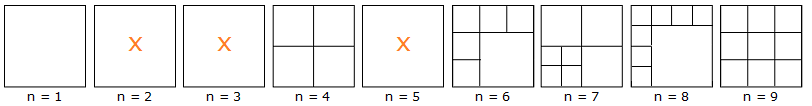
Bild 5
Zwischenstand:
- In Bild 5 mit den bereits behandelten Zerlegungen wurde n = 9 mit aufgenommen, weil uns das schon aus der Aufgabenstellung bekannt war.
- Vorsicht: Damit sind Q6 ... Q9 noch nicht geklärt, da wir noch nicht wissen, aus wievielen Äquivalenzklassen die Qn bestehen. Dies wird in Aufgabe 3 behandelt, wo wir für die einzelnen n untersuchen, ob es noch weitere Lösungen als die in Bild 5 dargestellten gibt.
- Für n > 9 kennen wir jetzt schon viele Zerlegungen, nämlich für alle geraden und für alle quadratischen n . Insbesondere kennen wir für n = 14 schon zwei verschiedene Lösungen.
Aufgabe 2
n > 8
Der Schlüssel zu den großen n liegt bei n = 7 . In Aufgabe 1 haben wir die Lösung für n = 4 genommen und ein Teilquadrat geviertelt; damit erhielten wir drei zusätzliche Teilquadrate. Aber das geht natürlich nicht nur bei n = 4 , sondern für beliebige n .
Regel C: n → n + 3 Aus einem Element von Qn lässt sich durch Viertelung eines Teilquadrates ein Element von Qn+3 generieren.
Da wir aus Aufgabe 1 bereits Lösungen für n = 6, ..., 9 kennen, sind die Qn für alle n ≥ 6 nicht-leer. Mit den Regeln B und C erhalten wir für einige n sogar mehrere Elemente von Qn ; siehe Bild 6:
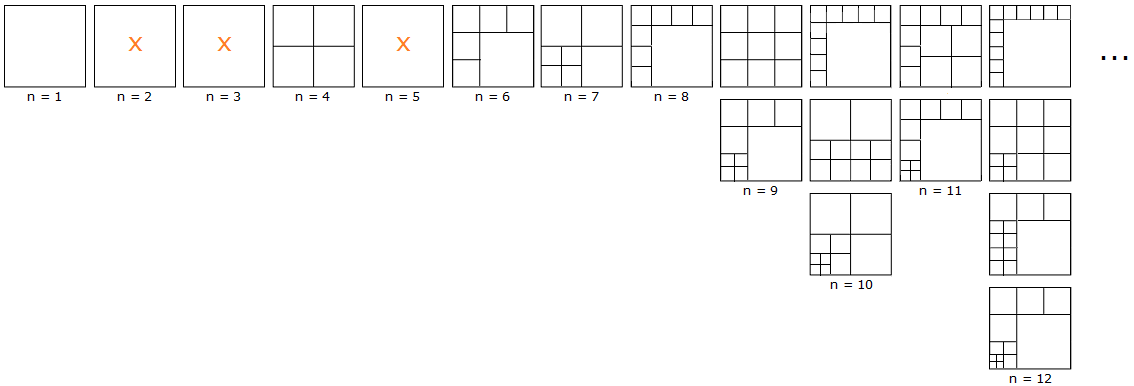
Bild 6
Aufgabe 3
Eindeutigkeit und Quasi-Eindeutigkeit
Offenbar gilt |Q1| = |Q4| = 1 , und die einzige Äquivalenzklasse enthält jeweils genau ein Element (siehe die Konstruktion für n = 4 in Aufgabe 1); für n = 1 und n = 4 gibt es also keinerlei Varianten.
|Q2| = |Q3| = |Q5| = 0 nach Aufgabe 1.
Für n ≥ 9 ist |Qn| > 2 . Anhand von Bild 6 kann man das sehen. Bei n = 9 und n = 11 können die kleinen Quadrate auch an anderer Stelle stehen. Für n ≥ 13 kann man immer auf n - 3 zurückgreifen.
Es bleiben noch die interessanten Fälle n = 6, 7, 8 zu untersuchen.
Aufgabe 1 hat mittels Konstruktion gezeigt, dass es nur eine einzige Äquivalenzklasse für n = 6 gibt, siehe die Lösung in Bild 6. Also ist |Q6| = 1 . Da das große Quadrat in jeder der vier Ecken liegen kann, besteht diese Äquivalenzklasse aus 4 Elementen.
Für n = 7 sehen wir eine Lösung in Bild 6. Ist sie (quasi-)eindeutig? - Wir erinnern uns an Regel A und den Tipp dazu in der Aufgabenstellung. Es muss (mindestens) eine Seite des Ursprungsquadrats von genau zwei Teilquadraten belegt werden; wir wählen o.E. die rechte Seite und als Seitenlängen der beiden Quadrate a und 1-a . Wir unterscheiden zwei Fälle: a = 0,5 und (o.E.) a > 0,5 .
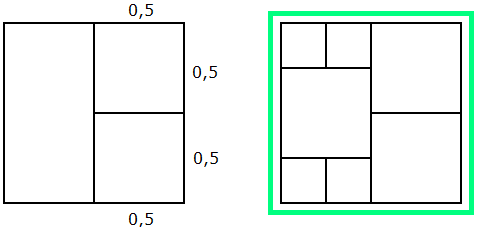
Bild 7 n = 7 , 1. Fall
1. Fall: a = 0,5 . Liegen im linken Rechteck (Bild 7) vier disjunkte Quadrate in den vier Ecken, so müssen diese alle die Seitenlänge 0,25 haben, denn es bleibt nur noch ein Teilquadrat übrig, das sowohl an die linke als auch an die rechte Rechteckseite anstoßen muss (siehe rechte Skizze in Bild 7). Damit haben wir eine andere Äquivalenzklasse als in Bild 6 geschaffen, aber unter Verwendung der gleichen Teilquadrate; auch diese Äquivalenzklasse besteht offenbar aus 4 Elementen. - Liegen im linken Rechteck (Bild 7) nur drei disjunkte Quadrate in den vier Ecken, so muss eines davon die Seitenlänge 0,5 haben; dies führt auf unsere erste Lösung in Bild 6.
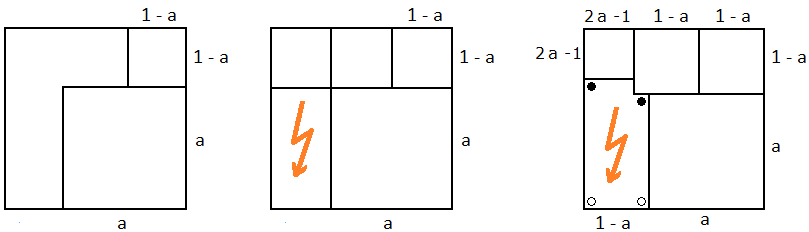
Bild 8 n = 7 , 2. Fall
2. Fall: a > 0,5 . Am linken und am oberen Rand müssen je mindestens drei Teilquadrate angrenzen, da 1-a < 0,5 ist (linke Skizze in Bild 8). An (mindestens) einem dieser beiden Ränder können es nur genau drei sein (denn anderenfalls wäre n > 7 ). Sei dies (o.E.) der obere Rand. Es können nicht alle drei angrenzenden Teildreiecke gleich groß sein, denn sonst wäre a = 2/3 und im übrig gebliebenen Rechteck links unten (mit dem Seitenverhältnis 1:2 ) könnten nicht drei Quadrate untergebracht werden (siehe die zweite Skizze in Bild 8). Also ergibt sich ein Bild wie in der dritten Skizze in Bild 8, mit 1-a > 1/3 . Dies führt zu einem Widerspruch, denn für die Ecken mit den schwarzen Punkten werden zwei Quadrate benötigt (das linke mit Seitenlänge 2a - 1 ), so dass unten links nur ein Quadrat der Seitenlänge 1-a mit den Ecken an den weißen Punkten liegen kann; dann wäre aber der linke Rand von der Länge 2·(2a-1)+ (1-a) = 3a - 1 , also a = 2/3 wie in der zweiten Skizze.
Wir haben also mit n = 7 einen quasi-eindeutigen Fall gefunden.
Für n = 8 haben wir in Aufgabe 1 eine Lösung erhalten, indem wir die Analogie zu n = 6 ausgenutzt haben (siehe Bild 6). Man kann aber auch den Lösungsweg für n = 7 aus dieser Aufgabe 3 verwenden. Die rechte Skizze in Bild 8 kann für n = 8 genutzt werden, wenn auch in den Ecken mit den weißen Punkten je ein Teilquadrat liegt. Es liegt nahe, für diese Teilquadrate einen Versuch mit gleichen Seitenlängen (1-a)/2 zu machen. Oberhalb dieser beiden Quadrate muss dann ein Quadrat der Seitenlänge 1-a liegen, das zu dem rechten schwarzen Punkt gehört. Zum linken schwarzen Punkt muss also ein Quadrat der Seitenlänge 1-(2a-1)-(1-a)-(1-a)/2 = (1-a)/2 gehören; diese Seitenlänge muss nach Bild 8 aber auch 2a - 1 betragen. Daraus erhalten wir a = 3/5 , was auf die Lösung in der linken Skizze von Bild 9 führt:
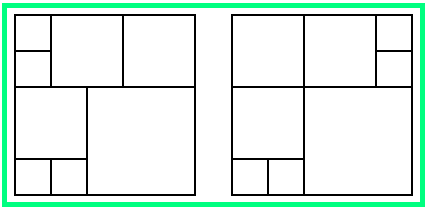
Bild 9 Zwei weitere Lösungen für n = 8
Die Seitenlängen der Teilquadrate in Bild 8 sind 1/5, 2/5 und 3/5 . Die Lage der kleinen Quadrate lässt sich auf mehrere Weisen verschieben (ein Beispiel dafür sieht man in der rechten Skizze von Bild 9), so dass man weitere Äquivalenzklassen erhält.
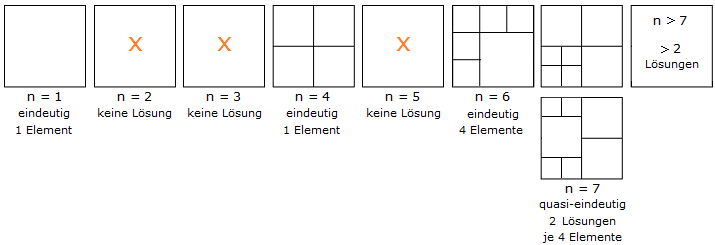
Zusammenfassung
0 Äquivalenzklassen
n = 2 keine Lösung
n = 3 keine Lösung
n = 5 keine Lösung
1 Äquivalenzklasse → Eindeutigkeit
n = 1 Klasse mit 1 Element
n = 4 Klasse mit 1 Element
n = 6 Klasse mit 4 Elementen
2 Äquivalenzklassen
n = 7 einziger Fall für Quasi-Eindeutigkeit beide Klassen mit je 4 Elementen
> 2 Äquivalenzklassen
n ≥ 8
|
Publiziert 2022-01-04 Stand 2019-04-18
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite