Wo geht die Sonne auf ?
Die Lösung steht im unteren Teil der Seite.
Gefragt wird hier nach der Himmelsrichtung, in der die Sonne aufgeht. Diese lässt sich am einfachsten im Gradmaß entlang des Horizonts angeben, und als Bezugspunkt wollen wir die Südrichtung nehmen. Geht z.B. die Sonne genau im Osten auf, so ist der Winkel auf dem Horizont zum Südpunkt t = 90° ; geht sie im Nordosten auf, ist t = 135° usw.
Die Beobachtung zeigt, dass dieser Winkel t von der Jahreszeit und vom Standort des Beobachters abhängt. Zur Veranschaulichung wählen wir das geozentrische Modell, das für unsere Zwecke einfacher und geometrisch äquivalent mit dem heliozentrischen Modell ist. Die Sonne bewegt sich in diesem Modell in einem Jahr entlang der Ekliptik auf einer "Himmelskugel" mit der Erde im Mittelpunkt, siehe Bild 1. Der Winkel ε ist die Neigung der Ekliptik; ε = 23,44°. Der Winkel δ ist die Deklination der Sonne, also der Breitengrad, über dem die Sonne senkrecht steht, somit gilt δ ∈[-ε,ε]. Wir werden der Einfachheit halber δ anstelle der Jahreszeit nehmen. Ist man an einem konkreten Datum interessiert, schaut man in einer tagesgenauen Umrechnungstabelle nach.
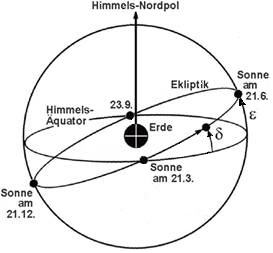
Bild 1
Copyright Graf-Zeppelin-Gymnasium Friedrichshafen, W. Seyboldt
In Bild 1 hat der Mittelpunkt die Koordinaten (0,0,0) in einem kartesischen (x,y,z)-Koordinatensystem. Die (x,y)-Ebene legen wir durch Erd-Äquator und Himmels-Äquator und die z-Achse durch die Pole.
Die Aufgabenstellung soll unter leicht idealisierten Annahmen behandelt werden:
Erde kugelförmig
Erdbahn kreisförmig
Erdradius gegenüber Abstand Erde - Sonne vernachlässigbar klein
kein Linseneffekt der Atmosphäre
Beobachter auf der Nordhalbkugel
Die ersten drei Annahmen führen nur zu unwesentlichen Verzerrungen der Ergebnisse.
Der Linseneffekt der Atmosphäre führt dazu, dass wir die Sonne bereits einige Minuten vor
ihrem eigentlichen Aufgang sehen. Dass wir nur die Nordhalbkugel betrachten wollen, stellt
keine Einschränkung dar, da alle Ergebnisse spiegelbildlich auch für die Südhalbkugel gelten.
1. Frage
Wie hängt der Sonnenaufgangspunkt vom Standort des Beobachters und von der Jahreszeit (Deklination der Sonne) ab ?
2. Frage
Wo auf der Erde liegen genau 90° zwischen den Sonnenaufgangspunkten zu Sommer- und Winteranfang ?
Lösung
1. Frage
Wie hängt der Sonnenaufgangspunkt vom Standort des Beobachters und von der Jahreszeit (Deklination der Sonne) ab ?
Das Studium von Bild 1 legt nahe, dass für den Standort des Betrachters lediglich der Breitengrad φ ∈[0°,90°] relevant ist. Also suchen wir eine Funktion t = f(φ,δ). Befindet man sich z.B. am 25. April auf dem 50. Breitengrad, der durch den Rheingau verläuft, so liefert die Umrechnungstabelle eine Deklination von 13°, d.h. die Sonne steht an diesem Tag über dem 13. Breitengrad senkrecht. t = f(50°,13°) ist dann der gesuchte Winkel zwischen dem Aufgangspunkt der Sonne und dem Süden.
In Bild 2 ist die Schnittebene durch die Himmelkugel für y = 0 abgebildet. Im Mittelpunkt steht die Erde. Da es hier nur auf Winkel, aber nicht auf Abstände ankommt, sei der Einfachheit halber der Radius der Himmelskugel (also der mittlere Abstand Erde - Sonne) zu 1 normiert.
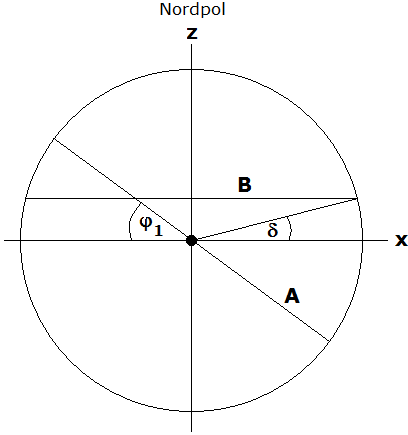
Bild 2
Zur Stellung der Sonne in Bild 2:
Die Sonne steht auf dem Breitengrad δ (Deklination) der Himmelskugel, also steht sie über dem irdischen Breitengrad δ senkrecht. δ schwankt zwischen ε = 23,44° (Sommeranfang) und -ε = -23,44° (Winteranfang). Die Sonne läuft an einem Tag durch einen Kleinkreis B auf der Himmelskugel (jedenfalls tut sie das in guter Näherung; in Wirklichkeit verändert sich δ während eines Tages geringfügig, um maximal 0,4°, wie man der Umrechnungstabelle entnehmen kann). Die Skizze zeigt B als gerade Linie, nämlich als die Projektion von B auf den Querschnitt.
Zum Standpunkt des Beobachters in Bild 2:
Der Betrachter möge auf dem Breitengrad φ stehen. Der Schnitt seiner Tangentialebene mit der Himmelskugel ist ein Großkreis und für ihn sein Horizont A ; in der Skizze sieht man A im Querschnitt als gerade Linie. Der Winkel φ1 in der Skizze ist dann φ1 = 90° - φ . Steht der Beobachter auf dem Äquator, steht A senkrecht (y-Achse, φ1 = 90°); steht er auf dem 45. Breitengrad (z.B. in Turin), sieht man A auf die 2. Winkelhalbierende in der Skizze projiziert; steht er auf dem Nordpol, ist φ1 = 0° und A waagerecht (Projektion entlang der x-Achse).
Der Schnitt durch die Himmelskugel in Bild 2 wurde so gelegt, dass die Sonne mittags in positiver x-Richtung und bei y = 0 steht (also am rechten Berührpunkt von B mit dem Kreis). Der für den Betrachter sichtbare Teils des Himmels ist die Halbkugel rechts oberhalb der Tangentialebene mit dem Rand A .
Mathematische Beschreibung von A :
Wir betrachten zunächst einen Spezialfall: Für φ = 90°, also φ1 = 0°, steht der Betrachter auf dem Nordpol und sieht die Nordhälfte der Himmelskugel. Der Horizont A ist dann der Äquator der Himmelskugel in der (x,y)-Ebene, siehe Bild 1; er kann durch die Parameterkurve (x,y,z) = (cos t, -sin t, 0) beschrieben werden. t ∈[0°, 360°) ist der Winkel, der entlang des Horizonts im Uhrzeigersinn gemessen wird, beginnend bei t = 0° mit (x,y,z) = (1,0,0); dies ist der Südpunkt oder "Mittagspunkt" (in der Skizze der ganz rechte Kreispunkt, wo der Kreis die x-Achse schneidet). Drei weitere Punkte auf dem Horizont des Nordpols sollen bezeichnet werden:
– Westpunkt ("Abendpunkt"): t = 90°, (x,y,z) = (0,-1,0); diesen Punkt muss man sich in Bild 2 vor der Zeichnungsebene liegend vorstellen, genau vor dem Mittelpunkt (also vor der Erde) im Abstand 1 .
– Nordpunkt ("Mitternachtspunkt"): t = 180°, (x,y,z) = (-1,0,0); linker Kreispunkt in Bild 2.
– Ostpunkt ("Morgenpunkt"): t = 270°, (x,y,z) = (0,1,0); diesen Punkt muss man sich in Bild 2 hinter der Zeichnungsebene liegend vorstellen, genau hinter dem Mittelpunkt (also hinter der Erde) im Abstand 1 .
In Bild 2 ist der Horizont A um den Winkel φ1 "verkippt", und zwar entlang der y-Achse als Drehachse. Dadurch bleiben die y-Koordinaten unverändert, und die Drehung betrifft die (x,z)-Koordinaten, also die Zeichnungsebene. Die Drehung um den Winkel φ1 erfolgt durch
(x,z)=(x,0) → (x cos φ1, -x sin φ1)
⇒ (x,y,z)=(x,y,0) → (cos t cos φ1, -sin t, -cos t sin φ1)
Dies ist die Beschreibung des Horizonts A in (x,y,z)-Koordinaten für t ∈[0°, 360°).
Beispiel: φ = 45° (Turin) → (x,y,z)=(√.5 cos t, -sin t, -√.5 cos t)
– Mittagspunkt (√.5, 0, -√.5)
– Abendpunkt (0,-1,0)
– Mitternachtspunkt (-√.5, 0, √.5)
– Morgenpunkt (0,1,0) Vorsicht: "Morgenpunkt" heißt nicht, dass dort die Sonne aufgeht.
Schnittpunkte A/B :
Die z-Komponente von B ist sin δ ⇒ -cos t sin φ1 = sin δ
⇒ cos t = -sin δ / sin φ1 = -sin δ / cos φ
Diese Gleichung hat zwei Lösungen t , die symmetrisch zu 180° liegen. Wendet man auf die Gleichung den arccos an, erhält man streng genommen nicht den Sonnenaufgangswinkel, sondern den Sonnenuntergangswinkel, denn arccos cos t = t gilt nur für t ∈[0°, 180°], also zwischen Mittagspunkt und Mitternachtspunkt. Da aus Gründen der Symmetrie beide Winkel betragsmäßig gleich groß sind und wir t vorzeichenlos definiert haben, erhalten wir:
(1) t = arccos(-sin δ / cos φ)
Zum Definitionsbereich von f(φ,δ) = arccos(-sin δ / cos φ): In der Klammer dürfen nur Werte vom Betrag ≤ 1 stehen, also muss für positive δ gelten: sin δ ≤ cos φ = sin(90°- φ). Dies ist äquivalent zu δ ≤ 90°- φ .
Daraus folgt, dass in den Tropen und den gemäßigten Breiten der Winkel t für jede Sonnendeklination δ berechnet werden kann. Nur für die Polarregionen ergibt sich eine Einschränkung des Definitionsbereiches von f , nämlich |δ| ≤ 90°- φ ; siehe auch die Erklärung unter Bild 5.
Das ist im Wesentlichen die Lösung der 1. Frage. Die rechte Seite von (1) ist die gesuchte Funktion f(φ,δ). Aber Vorsicht: Wir werden noch zeigen, dass (1) zwar für die gesamte nördliche Halbkugel hergeleitet wurde, diese Formel aber nur zwischen Wendekreis und Polarkreis, also in unseren gemäßigten Breiten, uneingeschränkt richtig ist; für die Tropen und die Polarregion wird im Folgenden noch ein ergänzender Kommentar gegeben.
In den Tropen ist φ ∈[0°, 23,44°] und φ1 ∈[66,56°, 90°]. Für δ > φ , also φ1 > 90° - δ , steht die Sonne mittags im Norden (siehe Bild 2). Der Winkel t wird aber in (1) vom Südpunkt aus berechnet. Will man das korrigieren, d.h. den Winkel zwischen Sonnenaufgangspunkt und Nordpunkt angeben, muss man 180° - t statt t nehmen.
In der Polarregion ist φ > 66,56° und φ1 < 23,44°. Bild 2 zeigt, dass für einen Teil des Jahres die Sonne den ganzen Tag über bzw. unter dem Horizont steht. Ist nämlich δ > φ1 = 90° - φ , so gibt es keinen Schnittpunkt von A und B (Sonne geht nicht unter). Und umgekehrt: Ist δ < -φ1 = φ - 90°, so gibt es ebenfalls keinen Schnittpunkt von A und B (Sonne geht nicht auf).
Die folgenden Skizzen dienen der Veranschaulichung der Formel (1) für t .
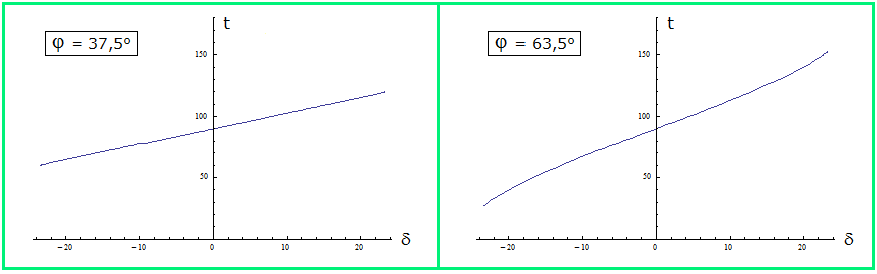
Bild 3 Zwei Graphen für die gemäßigten Breiten zwischen dem nördlichen Wendekreis auf φ = 23,44° und dem
Bild 3 nördlichen Polarkreis φ = 66,56° :
Bild 3 In beiden Skizzen ist die Deklination auf der waagerechten und der Winkel t des Aufgangspunkts der Sonne
Bild 3 zum Südpunkt auf der senkrechten Achse abgetragen, siehe (1). – Der linke Graph für die geographische Breite von
Bild 3 Catania auf Sizilien ist keine Gerade, sondern für δ < 0° leicht konkav und für δ > 0° leicht konvex; dies gilt
Bild 3 auch für alle folgenden Graphen.
Bild 3 Der rechte Graph zeigt den Winkel t für den Trondheimfjord in Norwegen.
Bild 3 Mit wachsendem δ (von links nach rechts also vom Winteranfang zum Sommeranfang) wächst der Winkel zwischen
Bild 3 Sonnenaufgangspunkt und Südpunkt streng monoton. Diese Steigung ist umso ausgeprägter, je weiter man nach
Bild 3 Norden kommt.
Bild 3 Liest man die Graphen von rechts nach links, erhält man den Winkel t vom Sommeranfang bis zum Winteranfang
Bild 3 (auch in Bild 4 und Bild 5).
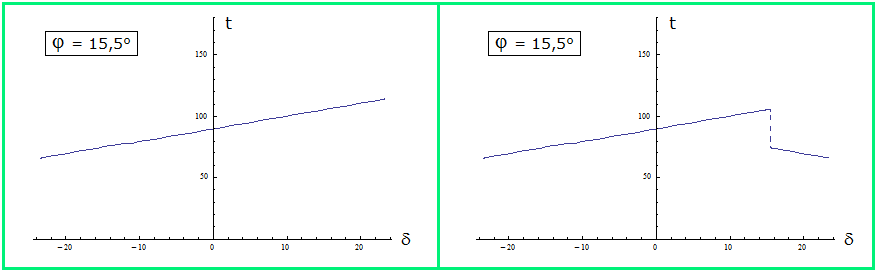
Bild 4 Beide Graphen zeigen den Winkel t für Khartum im Sudan; diese Stadt steht stellvertretend für die Tropen
Bild 3 zwischen dem Äquator auf φ = 0° und dem nördlichen Wendekreis auf φ = 23,44°.
Bild 3 Die linke Skizze ist aufgebaut wie in Bild 3.
Bild 3 Die rechte Skizze berücksichtigt, dass für δ > φ (in Khartum also im Hochsommer, genauer nach der
Bild 3 Umrechnungstabelle vom 3. Mai bis zum 10. August) die Sonne mittags im Norden steht, der Winkel
Bild 3 des Aufgangspunkts deshalb sinnvoller zum Nordpunkt gerechnet wird. Dort wird also statt des Winkels t
Bild 3 aus (1) der Winkel 180° - t genommen.
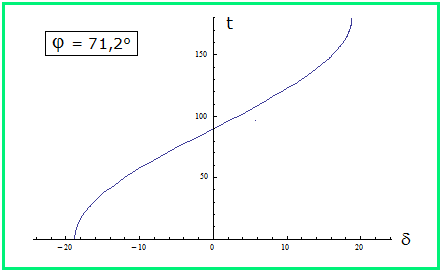
Bild 5 In der Polarregion zwischen dem nördlichen Polarkreis auf φ = 66,56° und dem Nordpol auf φ = 90°
Bild 3 – hier beispielhaft für das Nordkap skizziert – geht die Sonne für δ < φ - 90° nicht auf und für δ > 90° - φ
Bild 3 nicht unter.
Bild 3 Abgesehen von dem dadurch eingeschränkten Definitionsbereich entspricht der Graph der Darstellung in Bild 3.
Bild 3 Die Skizze zeigt, was sich im Laufe eines Jahres nördlich des Polarkreises am Himmel abspielt. Der Graph
Bild 3 – von links nach rechts gelesen – beginnt mitten im Winter (genauer bei δ = φ - 90°) mit t = 0° ;
Bild 3 an diesem Tag lässt sich die Sonne nur ganz kurz mittags genau im Süden blicken; am Nordkap ist das nach der
Bild 3 Umrechnungstabelle am 27. Januar . Danach wächst der Winkel (entlang des Horizonts gemessen), den die Sonne
Bild 3 an einem Tag überstreicht, kontinuierlich an bis zu einem Tag im Frühling (genauer bei δ = 90° - φ) mit t = 180°;
Bild 3 an diesem Tag scheint die Sonne 24 Stunden und berührt den Horizont nur ganz kurz um Mitternacht genau im Norden;
Bild 3 am Nordkap ist das nach der Umrechnungstabelle am 15. Mai .
Bild 3 Liest man den Graph von rechts nach links, so beginnt er an einem Tag im Sommer, nämlich wieder bei δ = 90° - φ ,
Bild 3 und endet an einem Herbsttag, wieder bei δ = φ - 90°; am Nordkap dauert diese Phase nach der Umrechnungstabelle
Bild 3 vom 30. Juli bis zum 16. November .
Bild 3 Zu δ = 0° gehört der Winkel t = 90° ; das bedeutet, dass bei Frühlings- und Herbstanfang die Sonne genau den halben
Bild 3 Horizont überstreicht (wie auch in Bild 3 und Bild 4).
Die Eigenschaften der Graphen in den Bildern 3 - 5 lassen sich durch zweifaches Ableiten von f nach δ nachweisen:
– f wächst mit δ .
– f ist konkav für δ < 0 , konvex für δ > 0 .
– Die Steigung von f (Ableitung nach δ) wächst auf dem gesamten Definitionsbereich mit φ .
Man vergleiche z.B. die beiden Graphen in Bild 3.
Die Ableitungen zum Nachrechnen:
fδ(φ,δ) = (cos δ)/(cos2 φ - sin2 δ)1/2 > 0
fδδ(φ,δ) = (sin δ sin2 φ)/(cos2 φ - sin2 δ)3/2
Weiter oben, am Anfang der Lösung, wurde der 25. April auf dem 50. Breitengrad als Beispiel genommen. Das Datum entspricht nach der Umrechnungstabelle einer Deklination δ = 13°. Mit (1) erhält man t = f(50°, 13°) = 110° 29' 6'', was natürlich wegen der bereits beschriebenen leichten Ungenauigkeit von (1) besser zu t = 110,5° gerundet werden sollte (und selbst dieser Wert würde sich bei einer Beobachtung in der Natur nur schwer exakt bestätigen lassen). Die Sonne geht also ungefähr in der Himmelsrichtung ONO (Ostnordost = 112,5° Abweichung von der Südrichtung) auf.
2. Frage
Wo auf der Erde liegen genau 90° zwischen den Sonnenaufgangspunkten zu Sommer- und Winteranfang ?
Für δ ist ± 23,44° in (1) einzusetzen:
tSommer = arccos(-s / cos φ) mit s = sin 23,44°
tWinter = arccos(s / cos φ)
Gefordert wird: tSommer - tWinter = 90°
Für die weitere Rechnung benötigen wir die Symmetrie des arccos :
arccos(-x) + arccos(x) = 180°
⇒ arccos(-x) - arccos(x) = 180° - 2 arccos(x)
90° = tSommer - tWinter = arccos(-s / cos φ) - arccos(s / cos φ) = 180° - 2 arccos(s / cos φ)
arccos(s / cos φ) = 45°
Mit dieser Gleichung – also mit tWinter = 45° – hätten wir auch oben beginnen können,
statt tSommer - tWinter zu berechnen. Denn wegen der Symmetrie des Sonnenlaufs zu den
Symmetriepunkten Frühlings- und Herbstanfang (siehe Bild 1 und Bild 2) muss tWinter
45° vom Ostpunkt entfernt sein und somit auch 45° vom Südpunkt.
Das bedeutet für den gesuchten Breitengrad φ :
Zu Winteranfang geht die Sonne exakt im Südosten auf und zu Sommeranfang exakt im Nordosten.
s / cos φ = 1/√2 ⇒ cos φ = s √2
φ = arccos s √2
Dies ist die Lösung der 2. Frage. Wir erhalten damit:
φ ≈ 55,767° ≈ 55°46'
Auf diesem Breitengrad liegen u.a. Moskau und die nördlichen Vororte von Kopenhagen. Nur auf diesem Breitengrad geht die Sonne zu Winteranfang exakt im SO und zu Sommeranfang exakt im NO auf. – Auf der Südhalbkugel liegt extrem wenig festes Land auf diesem Breitengrad, nämlich nur die drei chilenischen Inseln Wollaston, Freycinet und Ildefonso in der Nähe von Kap Hoorn; dort geht die Sonne zu Winteranfang (Vorsicht: Dann ist bei uns auf der Nordhalbkugel Sommeranfang!) exakt im NO und zu Sommeranfang exakt im SO auf.
Welchen Winkel überstreicht der Sonnenaufgang innerhalb eines Halbjahres hierzulande? Ein einfaches Beispiel liefert der 50. Breitengrad, der zentral durch Deutschland verläuft, auch durch den Rheingau. Wie bereits hergeleitet, gilt
tSommer - tWinter = 180° - 2 arccos(s / cos φ)
Dieser Ausdruck wächst offenbar streng monoton mit dem Breitengrad φ ; also ist bei uns tSommer - tWinter < 90° zu erwarten. Hier ist das exakte Ergebnis:
180° - 2 arccos(s / cos 50°) ≈ 76,46°
Kategorie: Geomathematik
Publiziert 2021-06-08 Stand 2017-08-14
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite




