Aufsteigende Würfel 1

          Die Lösung steht im unteren Teil der Seite.

Für ein bestimmmtes Spiel werden sechs Würfel benötigt. Sie erhalten verschiedene "Gewichte": Einer der Spielwürfel zählt standardmäßig von 1 bis 6, bei den anderen wird die geworfene Augenzahl mit 2, 3, 4, 5 bzw. 6 multipliziert ("gewichtet"). Damit man sie unterscheiden kann, haben die Würfel verschiedene Größen wie in Bild 1 (je größer der Würfel, desto größer der Gewichtsfaktor, aber das wird erst im 2. Teil dieses Problems eine Rolle spielen).



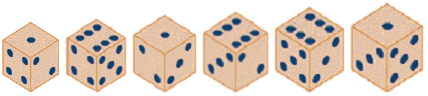
Bild 1


Für das Spiel müssen die gewichteten Augenzahlen zu "Punkten" addiert werden. Dies ergibt in Bild 1

1·1 + 2·6 + 3·1 + 4·6 + 5·6 + 6·1 = 76 Punkte


Aufgabe 1

Berechnen Sie den Erwartungswert und die Varianz der Wahrscheinlichkeitsverteilung für die Punkte. Die Verteilung selbst soll dafür nicht herangezogen werden.


Aufgabe 2

Zeigen Sie, dass die Wahrscheinlichkeitsverteilung symmetrisch ist. Was bedeutet das für den Median?


Aufgabe 3

Berechnen Sie die Wahrscheinlichkeitsverteilung (mit Hilfe eines Programms).


Aufgabe 4

Wie gut lässt sich die Wahrscheinlichkeitsverteilung durch eine Normalverteilung approximieren?

Lösung

Aufgabe 1

Berechnen Sie den Erwartungswert und die Varianz der Wahrscheinlichkeitsverteilung für die Punkte. Die Verteilung selbst soll dafür nicht herangezogen werden.

Für einen normalen und fairen Spielwürfel berechnet man leicht  7/2  als Erwartungswert und  35/12  als Varianz. Der  n-te Würfel hat dann  n·7/2  als Erwartungswert und  n²·35/12  als Varianz. Man geht von der Unabhängigkeit der Augenzahlen auf den sechs Würfeln aus und erhält als Gesamt-Erwartungswert bzw. Gesamt-Varianz die Summe der sechs einzelnen Erwartungswerte bzw. Varianzen:

μ = 147/2 = 73,5      σ² = 3185/12 = 265,41666...


Aufgabe 2

Zeigen Sie, dass die Wahrscheinlichkeitsverteilung symmetrisch ist. Was bedeutet das für den Median?

Den Definitionsbereich der Verteilung bilden die natürlichen Zahlen von  21  bis  126 . Die Verteilung wollen wir  P  nennen. Für die Symmetrie ist zu zeigen:

P(21+i) = P(126-i), i = 0,1,...,52

#(j) soll die Anzahl derjenigen Ergebnisse beim Würfeln sein, die  j  Punkte ergeben. Insgesamt gibt es  6⁶ = 46656  solcher Ergebnisse. Somit ist

P(j) = #(j)/46656

Es reicht also zu beweisen, dass

#(21+i) = #(126-i), i = 0,1,...,52

Wir wollen das zunächst an einem Beispiel zeigen. Für  i = 6  müsste  #(27) = #(120) sein. Wir rechnen das nach und erhalten jeweils  10  Ergebnisse:

a b c d e f

1 1 1 1 1 2
1 1 3 1 1 1
1 2 1 2 1 1
1 4 1 1 1 1
2 1 1 1 2 1
2 2 2 1 1 1
3 1 1 2 1 1   denn   1·3 + 2·1 + 3·1 + 4·2 + 5·1 + 6·1 = 27 , die anderen analog
3 3 1 1 1 1
4 1 2 1 1 1
5 2 1 1 1 1

2 5 6 6 6 6
3 6 5 6 6 6   denn   1·3 + 2·6 + 3·5 + 4·6 + 5·6 + 6·6 = 120 , die anderen analog
4 4 6 6 6 6
4 6 6 5 6 6
5 5 5 6 6 6
5 6 6 6 5 6
6 3 6 6 6 6
6 5 6 5 6 6
6 6 4 6 6 6
6 6 6 6 6 5

Somit ist  #(27) = #(120) = 10 . Man erhält aber nicht nur die selbe Zahl von Würfelergebnissen, sondern auch eine Symmetrie bei den Augenzahlen: Bei der ersten Zeile für  27  Punkte und der letzten Zeile für  120  Punkte handelt es sich jeweils um gegenüberliegende Augenzahlen; wenn z.B. die  1  oben liegt, liegt die  6 (unsichtbar) unten. Das gleiche gilt für die zweite Zeile für  27  Punkte und die vorletzte Zeile für  120  Punkte usw. Gegenüberliegende Augenzahlen addieren sich zu  7 . Also gehört zu jedem Würfelergebnis (a,b,c,d,e,f) mit  27  Punkten genau eines mit  120  Punkten, nämlich (7-a,7-b,7-c,7-d,7-e,7-f) (entsteht durch Umdrehen der Würfel). Wir wollen das nachrechnen:

1·a + 2·b + 3·c + 4·d + 5·e + 6·f = 27   ⇔   1·(7-a) + 2·(7-b) + 3·(7-c) + 4·(7-d) + 5·(7-e) + 6·(7-f) = 21·7 - 27 = 120

Wir verlassen nun das Beispiel und verallgemeinern die eben gezeigte Äquivalenz:

1·a + 2·b + 3·c + 4·d + 5·e + 6·f = 21 + i   ⇔   1·(7-a) + 2·(7-b) + 3·(7-c) + 4·(7-d) + 5·(7-e) + 6·(7-f) = 21·7 - (21 + i) = 126 - i

Also gilt  #(21+i) = #(126-i).

Aus der Symmetrie der Verteilung folgt, dass der Median gleich dem Erwartungswert  73,5  ist.


Aufgabe 3

Berechnen Sie die Wahrscheinlichkeitsverteilung (mit Hilfe eines Programms).

Aus Aufgabe 2 wissen wir:

P(j) = #(j)/46656

#(j) ist die Anzahl der Lösungen der Gleichung

1·a + 2·b + 3·c + 4·d + 5·e + 6·f = j

Die sechs auftretenden Variablen sind der Menge  {1,2,3,4,5,6}  zu entnehmen.  -  Dabei lässt man sich besser von einem Programm helfen. In Mathematica geht das mit dem Befehl  Reduce . Die Verteilung ergibt das folgende Bild.



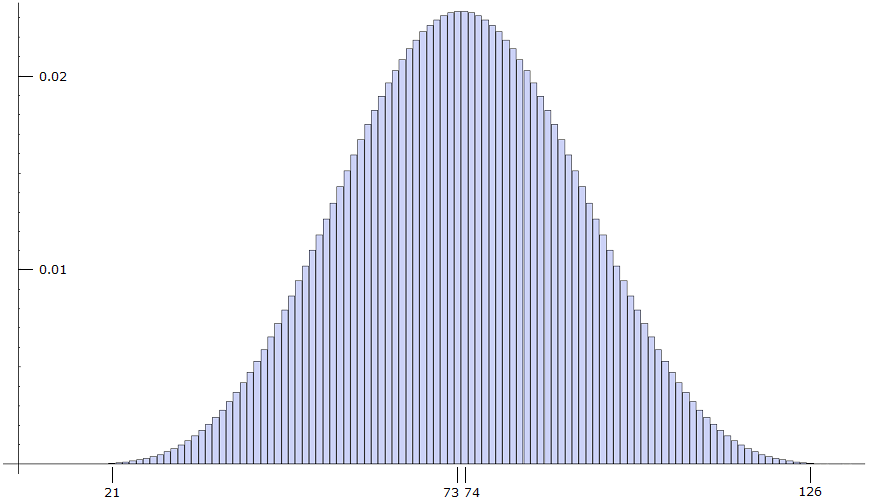
Bild 2

Die Glockenform der Verteilung lässt vermuten, dass eine gute Approximation durch eine Normalverteilung möglich ist. Das führt zur nächsten Aufgabe.


Aufgabe 4

Wie gut lässt sich die Wahrscheinlichkeitsverteilung durch eine Normalverteilung approximieren?

Der naheliegende Weg, die "passende" Normalverteilung zu finden, ist die Übernahme von  μ  und  σ  aus Aufgabe 1 für die Parameter der Normalverteilung. Man erhält dann das folgende Bild:



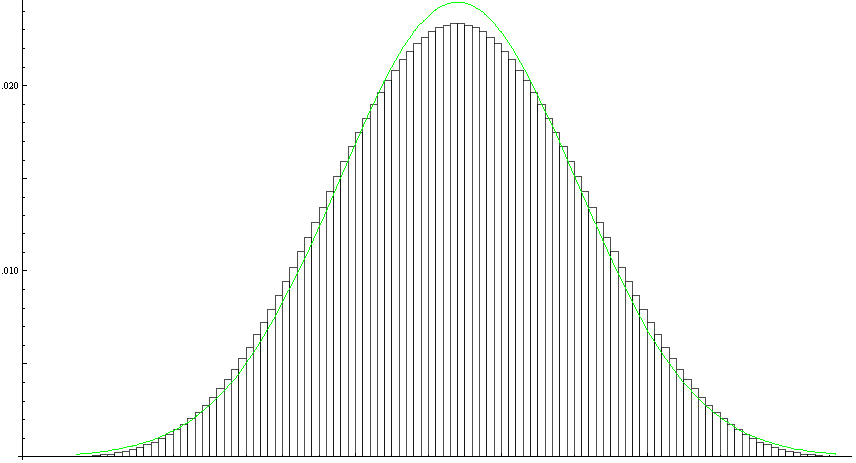
Bild 3

Die grüne Kurve in Bild 3 ist der Graph der Dichte  P_NV  der Normalverteilung. Das Ergebnis ist leicht enttäuschend, denn besonders gut sieht die Näherung nicht aus. Wir wollen vier Gütemaße berechnen, um die Qualität der Approximation zu quantifizieren:

abs-mittel = durchschnittliche absolute Abweichung
abs-max = maximale absolute Abweichung
rel-mittel = durchschnittliche relative Abweichung
rel-max = maximale relative Abweichung

Das muss präzisiert werden. Es wird für jedes  j ∈ {21, 126}  der Wert  P(j) (entspricht den einzelnen Balkenflächen) verglichen mit der zugehörigen Fläche  N_j  unter der Normalverteilung:

N_j = ∫_{j-.5 < x < j+.5} P_NV(x)dx

Die absolute Abweichung ist  |P(j)- N_j|  und die relative Abweichung ist  |P(j)- N_j|/P(j). Der Durchschnitt bzw. das Maximum wird dann über alle  j  genommen. Damit erhalten wir:

abs-mittel ≈ 0,000438
abs-max ≈ 0,00115
rel-mittel ≈ 0,509
rel-max ≈ 6,737

Die maximale absolute Abweichung von ca.  0,00115  findet man bei  j = 73  und  j = 74 .

Die relative Abweichung zeigt deutlich auf, warum die Normalverteilung keine gute Näherungsverteilung für  P  ist. Wir wollen das zur Verdeutlichung in  %  ausdrücken: Im Mittel weicht der Normalverteilungswert  N_j  um ca.  50,9 %  vom wahren Wert  P(j) ab; und im Maximum beträgt die Abweichung ca.  673,7 %  vom wahren Wert (diese Abweichung findet man bei  j = 22  und  j = 125 ) .

Publiziert 2016-12-26          Stand 2015-11-25

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem