Helle Sommertage


Zu Frühlings- und Herbstanfang dauern Tag und Nacht überall auf der Erde genau 12 Stunden.

Hier und im folgenden verstehen wir unter "Tag" die Zeitspanne zwischen Sonnenaufgang und -untergang. Es wird der Einfachheit halber unterstellt, dass die Erde kugelförmig ist und dass optische Verzerrungen durch die Lufthülle der Erde unberücksichtigt bleiben  -  beide Annahmen verfälschen die numerischen Ergebnisse des hier vorgestellten Problems nicht erheblich.

An anderen Tagen ist das nicht so. In Deutschland dauert z.B. der Tag im Sommer länger als die Nacht; am extremsten ist dies zu Sommeranfang zu beobachten. Dieser Effekt verstärkt sich, wenn man weiter nach Norden fährt. Nördlich des Polarkreises gibt es Tage, die 24 Stunden dauern, wo also die Nacht völlig ausfällt. Im Winter ist es gerade umgekehrt, da sind in Deutschland und nördlich davon die Nächte länger als die Tage.

Abgesehen vom Äquator, wo immer Tag- und Nachtgleiche herrscht, kann man überall auf der Erde im Jahresverlauf unterschiedliche Tages- und Nachtlängen beobachten.

Wir wollen nun der Einfachheit halber nur die Nordhalbkugel betrachten  -  auf der Südhalbkugel gibt es jeweils symmetrische Effekte.

Wo dauert zu Sommeranfang der Tag genau doppelt so lang wie die Nacht?

Lösung

Wir schauen uns in Bild 1 den Querschnitt der Erde durch die Polachse zu Frühlings- bzw. Herbstanfang (links) und zu Sommeranfang (rechts) an:


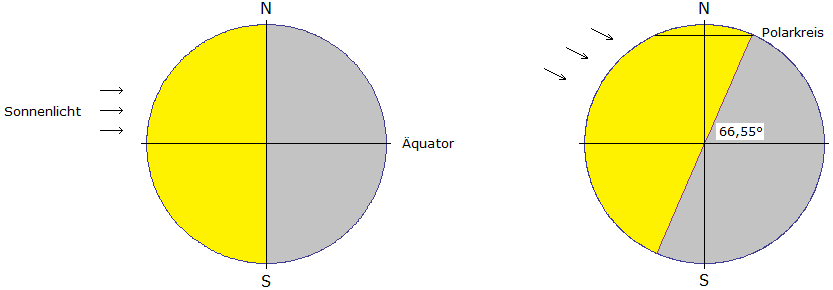
Bild 1


Die rechte Skizze in Bild 1 wird in Bild 2 links detaillierter dargestellt. Es wurde ein Breitengrad  φ  ergänzt. Wir können den Erdradius als  1  annehmen; damit lassen sich zwei Strecken bestimmen (sin φ  und  cos φ).  cos φ  ist der Radius des Kleinkreises, auf dem der Breitengrad verläuft.  x  ist eine Hilfsgröße, die später berechnet wird.

Rechts in Bild 2 ist der Breitenkreis vom Nordpol betrachtet abgebildet ("Draufsicht"). Hier finden wir den Radius  cos φ  und die Strecke  x  wieder. Nun wird die eigentliche Bedingung des Problems verwendet, nämlich dass der Tagbogen doppelt so lang ist wie der Nachtbogen.  x  muss gerade so groß gewählt werden, dass rechts von der rechten senkrechten Linie ein Drittel des Kreisumfangs liegt. Dies entspricht  120° , also hat das gepunktete Dreieck am Kreismittelpunkt den Winkel  60° .


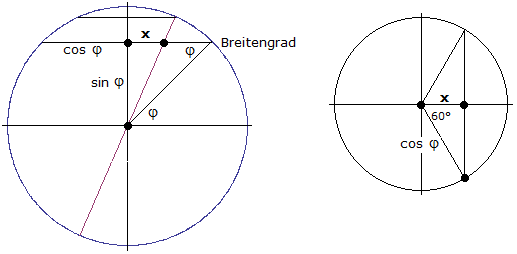
Bild 2

Nun können wir  x  auf zwei Weisen ausdrücken: Das linke gepunktete Dreieck hat am Kreismittelpunkt den Winkel  23,45°  (siehe Bild 1 rechts). Also ist

x/sin φ = tan 23,45°

Aus dem rechten gepunkteten Dreieck liest man ab:

x/cos φ = cos 60° = 1/2

Aus den beiden Gleichungen folgt durch Auflösen nach  x :

2 tan φ = cot 23,45°

φ = arctan((cot 23,45°)/2) ≈ 49,057°


Wir sind also fast genau auf dem 49. Breitengrad gelandet, auf dem u.a. Karlsruhe liegt und der einen großen Teil der Grenze zwischen den USA und Kanada bildet. Dort dauert der Tag zu Sommerbeginn doppelt so lang wie die Nacht.


Kategorie: Geomathematik

Publiziert 2014-12-30          Stand 2014-04-13

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem