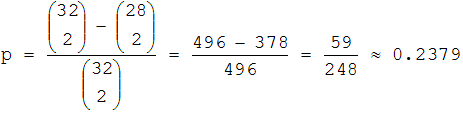
Was versteht man unter einem fairen Einsatz x , wenn a die Auszahlung im Gewinnfall ist (in unserem Beispiel also a = 1000 ) ? Der Betrag x geht vom Spieler an den Anbieter und wird auf keinen Fall zurückgegeben, also auch nicht im Gewinnfall. Im Verlustfall geschieht weiter nichts; im Gewinnfall zahlt der Anbieter den Betrag a an den Spieler aus. x heißt fair, falls der Erwartungswert g für den Gewinn (Auszahlung minus Einsatz) gleich 0 ist; für diesen Erwartungswert wird der Gewinnfall mit p und der Verlustfall mit 1 - p gewichtet:
g = p·(a-x) + (1-p)·(-x) = p·a - x = 0 → x = p·a
Folglich müsste Zweistein 237,90 Euro (auf volle Cent gerundet) einsetzen.
Im zweiten Teil des Problems geht es um bedingte Wahrscheinlichkeiten. Denn jetzt lauten die Fragen:
Mit welcher Wahrscheinlichkeit p1 ist ein Ass unter den gezogenen Karten, falls diese ein Pik enthalten?
Mit welcher Wahrscheinlichkeit p0 ist ein Ass unter den gezogenen Karten, falls diese kein Pik enthalten?
Wir vereinbaren ein paar Notationen:
A : (Mind.) ein Ass vorhanden
E1 : (Mind.) ein Pik vorhanden
E0 : Kein Pik vorhanden
p(A|Ej) : Bedingte Wahrscheinlichkeit für A unter der Voraussetzung, dass Ej vorliegt (j = 1 oder j = 0)
Hier ist die Formel für bedingte Wahrscheinlichkeiten:
p(A|Ej) = p(A ∩ Ej)/p(Ej)
Dabei ist p(Ej) die Wahrscheinlichkeit für Ej und p(A ∩ Ej) die Wahrscheinlichkeit für A und Ej .
Wir beginnen mit der Berechnung von p(Ej). Das geht ganz analog zur Berechnung von p . Unter den 496 möglichen Kombinationen sind 276 ohne Pik. Damit erhalten wir:

Für p(A ∩ Ej) müssen wir die Kartenpaare zählen, die sowohl ein Ass als auch ein Pik enthalten. Dafür lässt sich
- das Pik-Ass mit allen anderen 31 Karten kombinieren,
- jedes andere Ass ( 3 Karten) mit jedem anderen Pik ( 7 Karten) kombinieren.
Insgesamt erhalten wir 31 + 3·7 = 52 Kombinationen. Bei der Berechnung von p hatten wir benutzt, dass es 496 - 378 = 118 Kombinationen für das Ereignis A gibt. Für Ass und kein Pik verbleiben somit 118 - 52 = 66 Kombinationen.
Also ist p = p(A) = 118/496 , p(A|E0) = p(A ∩ E0)/p(E0) = (66/496)/(276/496) und p(A|E1) = p(A ∩ E1)/p(E1) = (52/496)/(220/496); dies ergibt gekürzt:
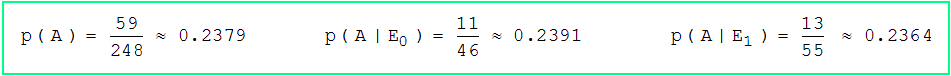
Dies ist das Hauptergebnis dieses Problems. Tatsächlich sind also die Ereignisse "Ass" und "Pik" nicht unabhängig. Die Zusatzinformation von Dreistein, dass ein Pik gezogen wurde, lässt die Wahrscheinlichkeit für ein Ass ein wenig sinken, während die Abwesenheit von Pik diese Wahrscheinlichkeit leicht erhöht.
Ganz allgemein heißen Ereignisse A und B unabhängig, wenn p(A ∩ B) = p(A)·p(B) ; dies lässt sich leicht umformulieren zu p(A) = p(A|B).
Diese Rechnung kann Zweistein zu seinem Vorteil ausnutzen. Er verwendet die folgende Strategie: Wenn er von Dreistein erfährt, dass ein Pik gezogen wird, spielt er gar nicht, denn die im Mittel zu erwartende Rückzahlung ist geringer als sein Einsatz:
p(A|E1)·a ≈ 236,36 → g = p(A|E1)·a - x ≈ -1,54 .
Mit der Information "kein Pik" akzeptiert Zweistein das Spiel und erhält im Schnitt
p(A|E0)·a ≈ 239,13 → g = p(A|E0)·a - x ≈ 1,23 .
Über alle Spielrunden, also auch die von Zweistein abgelehnten Spiele eingerechnet, gewinnt Zweistein ca. p0·1,23 ≈ 0,68 Euro pro Runde. Davon muss er fairerweise noch die Hälfte an seinen Helfer Dreistein geben. Natürlich sind ca. 34 Cent bei einem Einsatz von 1000 Euro wenig, aber hier ging es vorrangig um die Unabhängigkeit von Ereignissen. Auf den ersten Blick mag es durchaus so scheinen, als hätte der "Wert" einer Karte (hier das Ass) nichts zu tun mit der "Farbe" einer Karte (hier das Pik); also könnte man geneigt sein, die Information durch Dreistein als unerheblich anzusehen. Die Rechnung belehrt uns eines anderen.