Teilmengen


M  sei eine nicht-leere Menge mit  n  Elementen. Aus allen nicht-leeren Teilmengen von  M  werden zufällig zwei ausgewählt (die auch gleich sein dürfen).

Formal :  |M| = n > 0 ; (A,B) ∈ (P(M)\{Ø})²

a)  Mit welcher Wahrscheinlichkeit gilt  A ⊆ B ?

b)  Mit welcher Wahrscheinlichkeit gilt  A ⊆ B  oder  B ⊆ A ?

c)  Was ändert sich in a), b), wenn  A ⊂ B  bzw.  B ⊂ A  verlangt wird ?

d)  Mit welcher Wahrscheinlichkeit überdecken  A  und  B  die Menge  M  ( A ∪ B = M ) ?

e)  Mit welcher Wahrscheinlichkeit überdecken  A  und  B  die Menge  M  disjunkt  ( A ∪ B = M , A ∩ B = Ø ) ?

Lösung

Zur Vereinfachung wollen wir jede Teilmenge  C  von  M  als Menge von  n-Tupeln  c ∈ {0,1}ⁿ  darstellen. Ist  M = {m₁, m₂, ... , m_n} , so ist  c_i = 1  genau dann, wenn  m_i ∈ C .

Ist z.B.  n = 5 , so steht das Schema

A   1 1 0 1 1
B   0 1 0 0 1

für  A = {m₁, m₂, m₄, m₅}  und  B = {m₂, m₅} .

Ein solches Schema für zwei Teilmengen ist eine  (2×n)- Matrix. Da  A  und  B  nicht leer sein dürfen, gibt es  2ⁿ - 1  Möglichkeiten in jeder Zeile, somit  ( 2ⁿ - 1 )²  solcher Matrizen, also ebensoviele Auswahlen für  (A,B) .


a)  Mit welcher Wahrscheinlichkeit gilt  A ⊆ B ?

A ⊆ B  gilt, wenn in jeder Spalte der Matrix der untere Eintrag größer oder gleich dem oberen ist. Pro Spalte gibt es dafür drei Möglichkeiten, also insgesamt  3ⁿ . Darin sind allerdings die Matrizen enthalten, die in der oberen Zeile nur Nullen haben, das sind  2ⁿ  Stück. Insgesamt gibt es also  3ⁿ - 2ⁿ  erlaubte Matrizen. Die gesuchte Wahrscheinlichkeit beträgt somit :




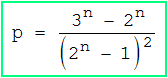
b)  Mit welcher Wahrscheinlichkeit gilt  A ⊆ B  oder  B ⊆ A ?

Wir verdoppeln zuerst die in a) gefundenen Möglichkeiten und streichen diejenigen, für die  A = B ≠ Ø  gilt (da diese doppelt gerechnet wurden); das ergibt  2·(3ⁿ - 2ⁿ) - (2ⁿ - 1)  erlaubte Matrizen. Die gesuchte Wahrscheinlichkeit beträgt somit :




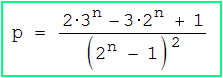
c)  Was ändert sich in a), b), wenn  A ⊂ B  bzw.  B ⊂ A  verlangt wird ?

Wir gehen wieder von den  3ⁿ  Matrizen aus a) aus. Da hier echte Teilmengen verlangt sind, werden zuerst die Matrizen mit  A = B  eliminiert, also  2ⁿ  Stück. Dann ist noch der Fall  A = Ø , B ≠ Ø  auszuschließen, dem 2ⁿ - 1  Matrizen entsprechen. Die Wahrscheinlichkeit für  A ⊂ B  ist also :



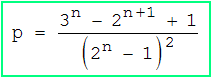
Werden in b) echte Teilmengen verlangt, muss man das eben erhaltene Ergebnis lediglich verdoppeln. Die Wahrscheinlichkeit für  A ⊂ B  oder  B ⊂ A  ist also :




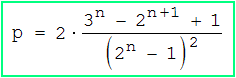
d)  Mit welcher Wahrscheinlichkeit überdecken  A  und  B  die Menge  M  ( A ∪ B = M ) ?

Eine Überdeckung von  M  liegt vor, wenn in jeder Spalte der Matrix mindestens eine  1  steht. Das ergibt pro Spalte drei Möglichkeiten, also insgesamt  3ⁿ . Darin sind allerdings die beiden Matrizen enthalten, die in der oberen Zeile nur Nullen und in der unteren nur Einsen bzw. umgekehrt. Insgesamt gibt es also  3ⁿ - 2  erlaubte Matrizen. Die gesuchte Wahrscheinlichkeit beträgt somit :




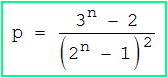
e)  Mit welcher Wahrscheinlichkeit überdecken  A  und  B  die Menge  M  disjunkt  ( A ∪ B = M , A ∩ B = Ø ) ?

Überdecken  A  und  B  die Menge  M  disjunkt, so folgt aus der Festlegung von  A  zwingend die komplementäre Teilmenge  B . Von den  2ⁿ  Möglichkeiten für  A  sind die beiden auszuschließen, die in einer Matrixzeile nur Nullen und in der anderen nur Einsen aufweisen, also  A = Ø  und  A = M . Die gesuchte Wahrscheinlichkeit ist daher :




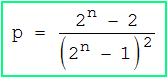
Beispiel  für  n = 6

Insgesamt gibt es  ( 2⁶ - 1 )² = 3969  mögliche Matrizen. Die folgenden Wahrscheinlichkeiten sind auch als Brüche angegeben, damit man die Anzahl der jeweils erlaubten Matrizen ablesen kann.

A ⊆ B   ⇒   p = 665/3969 ≈ 0,1675

A ⊆ B  oder  B ⊆ A   ⇒   p = 1267/3969 ≈ 0,3192

A ⊂ B   ⇒   p = 602/3969 ≈ 0,1517

A ⊂ B  oder  B ⊂ A   ⇒   p = 1204/3969 ≈ 0,3034

A ∪ B = M   ⇒   p = 727/3969 ≈ 0,1832

A ∪ B = M , A ∩ B = Ø   ⇒   p = 62/3969 ≈ 0,0156

Publiziert 2010-06-14          Stand 2009-11-09

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem

Manfred Börgens   |    zur Leitseite