Ein Modell für transitive Relationen

          Die Lösung steht im unteren Teil der Seite.

A, B  und C  sind leidenschaftliche Spieler und Liebhaber der Zahlen. Als sie eines Tages alle drei zu einer Fernseh-Spielshow eingeladen werden, verabreden sie  -  um die Sache noch interessanter zu machen  -  ihre Gewinne nachher untereinander neu zu verteilen. Diese Verteilung soll nach einem von ihnen ersonnenen "Vererbungsprinzip" für Primfaktoren erfolgen:

(1)
Bei den Beträgen, die nach der Show verteilt werden, soll es sich immer um natürliche Zahlen handeln, die nur die Primfaktoren  2, 3, 5  enthalten.

(2)
A's Zahl heißt  a  und muss den Faktor  p_A = 2  enthalten.
B's Zahl heißt  b  und muss den Faktor  p_B = 3  enthalten.
C's Zahl heißt  c  und muss den Faktor  p_C = 5  enthalten.
Die  p_X  wollen wir "Basisfaktoren" nennen.

(3)
Die drei Gewinne aus der Show (in der Regel verschieden, aber immer genügend groß) werden jeweils bis zur größten Zahl abgerundet, die (1) und (2) erfüllt. Die Reste verbleiben bei den Spielern und spielen danach keine Rolle mehr.

(4)
Vererbungsgesetz:
X, Y, Z  seien nun Platzhalter für die Spieler, und  x, y, z  die zugehörigen Platzhalter für die Beträge aus (2).
X → Y soll heißen:  " y  erbt alle Primfaktoren von  x "  und bedeutet für die Spieler "Y erhält einen Anteil von X's Gewinn".
Dies soll präzisiert werden:
X → Y     ⇔     x = 2^x2·3^x3·5^x5  und  y = p_Y·2^y2·3^y3·5^y5  mit  y_i > 0 , falls  x_i > 0 .
Man beachte, dass auch  X → X  auftreten kann.
Nochmal in Worten:  y  erbt alle Primfaktoren von  x  genau dann, wenn:
-  y  enthält (mindestens) jeden Primfaktor von  x  mindestens einmal.
-  Falls  x  den "fremden" Basisfaktor  p_Y  enthält, kommt dieser in  y  mindestens in zweiter Potenz vor.

Nun lässt sich leicht feststellen, an wen ein Spieler  X  etwas von seinem Gewinn abgeben muss. Die "Empfänger" (das können 0 bis 3 Personen sein, evtl. inklusive des "Gebers" X) teilen sich dann den Betrag  x  zu gleichen Teilen.

Zwei Beispiele:

• A  gewinnt in der Show 140 Euro,  B  gewinnt 100 Euro,  C  gewinnt 225 Euro. Dann ist  a = 128 (= 2⁷), b = 96 (= 2⁵·3), c = 225 (= 3²·5²) .
  Somit gilt:  A → A ,  A → B ,  C → C .
  Also muss  A  64 Euro an  B  abgeben.


• A  gewinnt 495 Euro,  B  gewinnt 730 Euro,  C  gewinnt 475 Euro. Dann ist  a = 486 (= 2·3⁵), b = 729 (= 3⁶), c = 450 (= 2·3²·5²) .
  Somit gilt:  A → C ,  B → A ,  B → B ,  B → C ,  C → C .
  A  muss also seinen (abgerundeten) Gewinn an  C  abgeben.  B  muss seinen (abgerundeten) Gewinn mit  A  und  C  teilen. Am Ende haben (incl. der einbehaltenen Rundungsreste)  A  252 Euro,  B  244 Euro und  C  1204 Euro.

	a = 22·3·5 b = 3 c = 2·52	111 000 101	A → A     B → A C → A     C → C
	a = 2·5 b = 2·3·5 c = 2·5	001 101 100	A → B     C → B
	a = 22·3 b = 2·32 c = 5	110 110 000	A → A     A → B B → A     B → B
	a = 22·3 b = 2·32 c = 2·5	110 110 100	A → A     A → B B → A     B → B

Frage 5
Wie hängen "Primfaktordarstellung" und "Schachteldarstellung" zusammen?
Dies lässt sich am einfachsten über den Code beschreiben.

Wir haben also zwei (miteinander verwandte) Modelle gefunden, die äquivalent zur Menge der transitiven Relationen auf einer dreielementigen Menge  M  sind. Was bedeutet diese Äquivalenz genau?

• Jeder transitiven Relation auf  M  entspricht eine Klasse von Tripeln. Umgekehrt gilt, dass alle diese Tripel eindeutig einer der transitiven Relation auf  M  zugeordnet werden können. Die Tripel können Zahlentripel  (a, b, c)  wie in (1), (2) oder Codes wie in (5) oder Schachteln wie in (6) sein.


• Dem Element  (X, Y)  einer transitiven Relation auf  M  entspricht die "Vererbung"  X → Y  im Modell.

Lösung

Zu Frage 1

512

Hat eine Menge  M  n  Elemente, so hat  M×M  n²  Elemente. Hat eine Menge  m  Elemente, so hat ihre Potenzmenge (Menge aller Teilmengen)  2^m  Elemente (da in den Teilmengen jedes Element entweder vorkommt oder fehlt). Hier ist  n = 3  und  m = n² = 9 , also hat  M×M  2⁹ = 512  Teilmengen.


Zu Frage 2

x  enthält  p_X  in mindestens zweiter Potenz.

Dies folgt direkt aus der Definition in (4).


Zu Frage 3

171

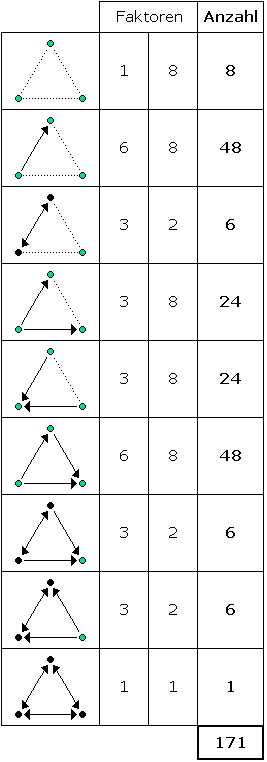
In der folgenden Tabelle sind die neun Grundtypen für transitive Relationen auf einer dreielementigen Menge als Graphen dargestellt. Da die Lage von  A, B, C  auf den drei Knoten der Graphen nicht spezifiziert ist, steht in der zweiten Spalte die Anzahl der Möglichkeiten für die Positionierung der Pfeile. Diese Anzahl ist z.B. beim zweiten Graphen gleich 6, weil man 3 Möglichkeiten für den Ursprung des Pfeils hat, und dann jeweils 2 Möglichkeiten für das Ziel des Pfeils; beim dritten Graphen kann der Doppelpfeil 2 von 3 Knoten verbinden, dafür gibt es 3 Möglichkeiten; usw. In der dritten Spalte sind die Möglichkeiten dargestellt, die sich aus der Färbung der grünen Punkte in schwarz oder weiß ergeben (es kommen nur 1, 2 und 2³ vor). Die Zahlen in der zweiten und dritten Spalte sind die Faktoren, die multipliziert in der vierten Spalte die Gesamtanzahl der Relationen ergeben, für die die einzelnen Graphen stehen.




Zu Frage 4

Die folgende Tabelle ist wie die Tabelle zu Frage 3 aufgebaut. Oben links steht die Struktur der Graphen: Für  X, Y, Z  kann man  A, B, C  in beliebiger Anordnung einsetzen;  p, q, r  sind dann beliebige (verschiedene) Primzahlen, die den  X, Y, Z  zugeordnet werden. Wird ein grüner Punkt zu einem weißen Punkt, so ist der zugehörige Exponent gleich  1 , da keine Schleife vorliegt. Wird ein grüner Punkt zu einem schwarzen Punkt, so steht er für eine Schleife und der zugehörige Exponent ist gleich  2  oder größer. Überall wurden möglichst einfache  x, y, z  gewählt. Eine vollständige Übersicht der möglichen  x, y, z  findet man unten bei der Zusatzaufgabe.




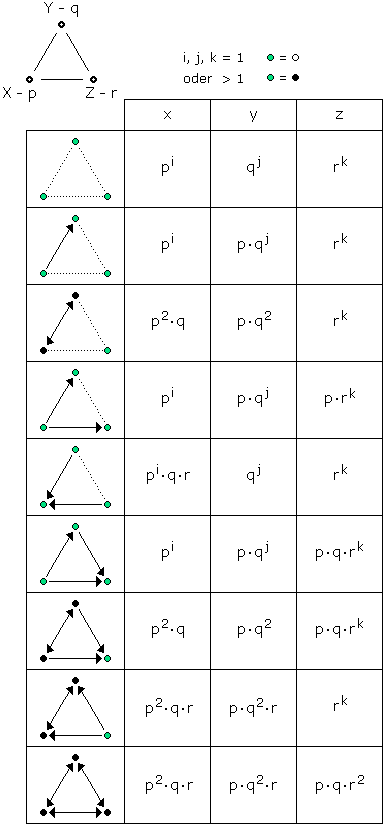
Zu Frage 5

Sei  a = p·pⁱ·q^j·r^k . Das erste Tripel im Code hat Nullen an den Stellen, für die der zugehörige Exponent gleich  0  ist, und Einsen sonst. Entsprechendes gilt für  b  und das zweite Tripel, sowie für  c  und das dritte Tripel. Damit lässt sich nun die "Schachteldarstellung" leicht angeben. Die drei Tripel stehen für die drei Schachteln:

A  ↔  1. Tripel  ↔  grüne Schachtel
B  ↔  2. Tripel  ↔  rote Schachtel
C  ↔  3. Tripel  ↔  schwarze Schachtel

Der Inhalt der Schachteln bestimmt sich aus dem zugehörigen Tripel: die erste Ziffer bestimmt, ob eine grüne Kugel vorhanden ist  ( 1 = ja,  0 = nein), analog für die beiden anderen Ziffern. Wir betrachten ein Beispiel:

a = p6·q9·r b = q c = p2·r2

111 000 101

Dieser Zusammenhang lässt sich auch in umgekehrter Reihenfolge lesen, also beginnend bei den Schachteln. Im Beispiel entspricht dem Code:

a = p^>1·q^>0·r^>0      b = q      c = p^>0·r^>1

Damit ist die Frage vollständig beantwortet.


Zusatzaufgabe

Wir haben schon bei den Beispielen unter (7) gesehen, dass zu einer transitiven Relation mehrere Darstellungen in Form der Codes gehören können. Ein kleines Programm hilft, eine vollständige Äquivalenzliste zu erzeugen. Diese ist hier in einer Übersicht ausgelagert.

Publiziert 2009-06-13          Stand 2008-09-28

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem