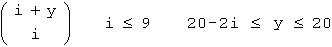Der Kalender des Planeten Biluna

          Die Lösung steht im unteren Teil der Seite.

Unser intergalaktischer Korrespondent berichtet:

Biluna ist ein bewohnter Planet in einem fernen Sonnensystem. Biluna wird von zwei Monden umkreist, Xeluna und Yluna.




Die Bewohner Bilunas führen ihren Kalender so wie wir auf der Erde: Sie zählen die Tage und die Jahre. Aber bei den Monaten waren sie etwas einfallsreicher. Da sie beide Monde gleichermaßen verehren, haben sie zwei verschiedene Monatslängen eingeführt: 21 Tage (ziemlich genau die Umlaufzeit von Xeluna) und 10 Tage (ziemlich genau die Umlaufzeit von Yluna). Ganz wichtig ist auf Biluna, dass Sonnen- und Mondkalender miteinander harmonieren, d.h. jedes Jahr besteht aus einer ganzen Zahl von Monaten; kein Tag darf übrigbleiben.

Wegen der Nähe von Biluna zu einem massereichen anderen Planeten treten Schwankungen in der Jahreslänge auf. Seit Einführung des Kalenders auf Biluna ist es aber immer gelungen, die Anzahl der Tage in einem Jahr vollständig auf Xeluna- und Yluna-Monate aufzuteilen.

Auf Biluna nennt man die Anzahl der Tage  n  in einem Jahr
-  kalendarisch, wenn sich die  n  Tage vollständig auf Xeluna- und Yluna-Monate aufteilen lassen, so dass Sonnen- und Mondkalender miteinander harmonieren;
-  kalendarisch eindeutig, wenn diese Aufteilung eindeutig ist (die Reihenfolge von Xeluna- und Yluna-Monaten im Jahr spielt dabei keine Rolle); ansonsten heißen kalendarische Zahlen mehrdeutig.

Auf Biluna sind auch Kalender erlaubt, die in einem Jahr nur gleich lange Monate vorsehen, also ausschließlich Xeluna-Monate, aber keine Yluna-Monate, oder umgekehrt.

Zur Zeit dieses Berichtes hat das Jahr eine Länge, die kalendarisch mehrdeutig ist. Im folgenden Jahr muss aber der Kalender umgestellt werden: Das Jahr wird einen Tag kürzer werden und deshalb eine andere Zusammenstellung von Xeluna- und Yluna-Monaten haben; die Jahreslänge wird dann eine kalendarisch eindeutige Zahl sein. Die Astronomen auf Biluna haben ausgerechnet, dass die nächste Umstellung noch einige Zeit auf sich warten lassen wird, aber es steht schon fest, dass dann das Jahr um einen weiteren Tag verkürzt werden muss; diese Änderung wird wieder auf eine kalendarisch mehrdeutige Tageszahl führen. Da die Bewohner Bilunas die Abwechslung lieben, werden sie in der langen kalendarisch eindeutigen Phase  -  also ab dem nächsten Jahr  -  die Reihenfolge der Xeluna- und Yluna-Monate ständig wechseln. Das stellt kein Problem dar, denn dafür gibt es etwa 10 Millionen Möglichkeiten.

Wie lang ist das aktuelle Jahr auf Biluna?

Lösung

Der Nachweis für diese Lösung erfordert eine Analyse des Biluna-Kalenders. Wir werden das etwas ausführlicher tun, als es für die eigentliche Problemlösung unbedingt nötig wäre.

n   Jahreslänge (Anzahl Tage)
x   Anzahl Xeluna-Monate (à 21 Tage)
y   Anzahl Yluna-Monate (à 10 Tage)

(1)  In kalendarischen Jahren ist  n = 21 x + 10 y .
Dies ist eine diophantische Gleichung, da nur ganzzahlige Lösungen  x, y  gesucht sind.

Wichtig ist zunächst die Beobachtung, dass die Endziffer von  n  nur durch  x  bestimmt wird, denn wegen der Faktoren  21  und  10  müssen die natürlichen Zahlen  n  und  x  die gleiche Endziffer  i  haben, falls eine Lösung existiert. Eine "Grundlösung" für (1) erhält man also immer mit  x = i  Xeluna-Monaten, da der Rest wegen des Faktors  10  mit Yluna-Monaten aufgefüllt werden kann. Weitere Lösungen können ggfs. mit  x = i + 10 k  gebildet werden ( k  natürliche Zahl).

Ein Beispiel:  n = 566  führt auf die Grundlösung  566 = 21·6 + 10·44  und die beiden weiteren Lösungen  566 = 21·16 + 10·23 = 21·26 + 10·2 .

Damit wird ein Muster sichtbar. Wenn man eine Grundlösung
n = 21 x₁ + 10 y₁  mit  x₁ = i
gefunden hat, lauten alle anderen Lösungen von (1):

(2)   n = 21 x₂ + 10 y₂  mit  x₂ = i + 10 k  und somit  y₂ = y₁ - 21 k .

Diese anderen Lösungen existieren für diejenigen positiven  k , für die  y₁ - 21 k  nicht negativ wird.

Eine eindeutige Lösung erhält man also, wenn nur die Grundlösung in Frage kommt, eine zweideutige Lösung, wenn in (2) nur  k = 1  in Frage kommt, eine dreideutige Lösung, wenn genau  k = 1  und  k = 2  in Frage kommen usw.

Wann gibt es keine Lösung? (D.h. wann ist ein Biluna-Jahr nicht-kalendarisch?) Wir bezeichnen mit  i  wieder die Endziffer der Jahreslänge  n . (1) ist offenbar nur dann mit nicht-negativem  y  lösbar, wenn  n - 21 i  ein nicht-negatives Vielfaches von  10  ist. Das Maximum für  i  ist  9 , somit ist  n = 179  die größte Zahl, die keine Lösung zulässt.

Wann ist die Lösung eindeutig? (D.h. wann ist ein Biluna-Jahr kalendarisch eindeutig?) Dann gibt es also nur die Grundlösung  n = 21 i + 10 y . Nach (2) muss  y - 21 < 0  sein. Aus  0 ≤ y ≤ 20  folgt
21 i ≤ n ≤ 21 i + 200
Demnach ist (für  i = 9 )  n = 389  die maximale Jahreslänge mit einer eindeutigen Lösung. Offenbar ist  n = 10  die minimale Jahreslänge mit einer eindeutigen Lösung.

Mehrdeutige Lösungen. Für genau  r > 1  Lösungen erhalten wir mit (2):
n = 21 i + 10 y
n = 21(i + 10) + 10(y - 21)
...
n = 21(i + 10(r-1)) + 10(y - 21(r-1))      mit  y ≥ 21(r-1) , aber  y < 21 r .

Aus  21(r-1) ≤ y ≤ 21 r - 1  folgt  21 i + 210(r-1) ≤ n ≤ 21 i + 210 r - 10 = 21 i + 210(r-1) + 200 . Das minimale  n  (für  i = 0 ) ist dann  210(r-1) , das maximale  n  (für  i = 9 ) ist  210(r-1) + 389 . Bei beiden  n  überzeugt man sich schnell, dass sie tatsächlich zu den Jahreslängen mit r-deutiger Lösung gehören.

Nun können wir uns wieder der ursprünglichen Problemstellung widmen und die in Frage kommenden Jahreslängen  n  stark einschränken. Wir suchen ein  n , für das  n - 1  kalendarisch eindeutig ist. Also ist  n - 1 ≤ 389 . Andererseits sind  n  und  n - 2  kalendarisch mehrdeutig, also ist  n - 2 ≥ 210 . Was kann uns bei der Suche nach kalendarisch eindeutigen Zahlen zwischen  211  und  389  helfen? Wegen  21 i + 10 y ≥ 211  ist   y ≥ 20 - 2 i . Es wurde außerdem die Information gegeben, dass es etwa 10 Millionen Möglichkeiten gibt, die Xeluna- und die Yluna-Monate zu kombinieren. Es gibt insgesamt  x + y  Monate, von denen die Xeluna-Monate  x = i  Positionen einnehmen. Dafür gibt es



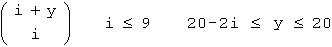
Möglichkeiten. Dieser Binomialkoeffizient wächst mit  i  und  y ; man stellt schnell fest, dass nur die maximal möglichen  i = 9  und  y = 20  auf eine Anzahl Kombinationen in der Nähe von  10.000.000  führen, genauer auf  10.015.005 .

So kommen wir auf das kalendarisch eindeutige  n - 1 = 21·9 + 10·20 = 389 . Zu überprüfen ist nur noch, ob  n = 390  (für das aktuelle Biluna-Jahr) und  n - 2 = 388  tatsächlich kalendarisch zweideutig sind. Im ersten Fall ist  i = 0  mit der Grundlösung  (x, y) = (0, 39)  und der weiteren Lösung  (x, y) = (10, 18) . Im zweiten Fall ist  i = 8  mit der Grundlösung  (x, y) = (8, 22)  und der weiteren Lösung  (x, y) = (18, 1) .

Publiziert 2009-04-19          Stand 2008-08-19

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem