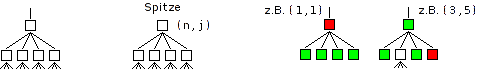Würfel-Nim
und ein Exkurs in die Theorie der endlichen Spiele
Die Lösung steht im unteren Teil der Seite.
Im Problem # 46 wurde bereits ein Nim-Spiel vorgestellt. Diesmal gehört ein Würfel dazu, mit dem aber nicht gewürfelt wird (mit Ausnahme der Spielvorbereitung), sondern der von den beiden Spielern nur gedreht wird. Hier sind die Spielregeln:
- Würfel-Nim ist ein Zwei-Personen-Spiel; die Spieler werden mit A und B bezeichnet.
- Vor Beginn des Spiels wird ein Zahlenpaar (n,j) festgelegt. n ist eine natürliche Zahl (nicht zu klein, n > 20 wäre gut). j wird gewürfelt, ist also eine natürliche Zahl zwischen 1 und 6 .
- Bestimmung von (n,j) :
A oder B wählt eine natürliche Zahl N . Durch Würfeln wird n = N - Augenzahl ermittelt. j wird ebenfalls durch Würfeln bestimmt. Dabei gibt es zwei Möglichkeiten:
Variante I: Der Würfel wird nur einmal geworfen. Die Augenzahl j dient gleichzeitig zur Ermittlung von n , also ist n = N - j .
Variante II: Der Würfel wird zweimal geworfen, um zuerst n = N - Augenzahl und dann j zu bestimmen.
- A beginnt das Spiel. A und B sind abwechselnd am Zuge. Nach jedem Zug wird ein neuer "Score" m berechnet. Vor dem ersten Zug ist der Score m = n .
- Der Spieler am Zuge dreht den Würfel über eine Kante seiner Wahl (4 Möglichkeiten) und bringt damit eine andere Augenzahl nach oben. Den neuen Score erhält man, indem man diese Augenzahl vom alten Score subtrahiert. Es wird vorausgesetzt, dass für diese Drehungen ein "regulärer" Würfel verwendet wird, der auf gegenüberliegenden Seiten jeweils die Augensumme 7 aufweist.
- Ende des Spiels: Verloren hat der Spieler, der durch seinen Zug als erster auf einen negativen Score kommt.

Drehung über eine Kante
Nur die Spielvorbereitung beruht auf Zufallsereignissen. Der eigentliche Spielverlauf liegt vollständig in der Hand der beiden Spieler, die also bemüht sein werden, erfolgreiche Strategien zu entwickeln.
Eine geeignete Notation für Würfel-Nim ist das Zahlenpaar (m,k) , das der Spieler am Zuge vorfindet, bevor er seinen Zug ausführt. (m,k) wird also vom Gegner "hinterlassen" oder "übergeben". Dabei steht m für den aktuellen Score und k für die Augenzahl, die der Würfel auf seiner Oberseite zeigt. Bei Spielbeginn findet A (m,k) = (n,j) vor. (m,k) heißt Gewinnposition, wenn es für den Spieler am Zuge eine Strategie gibt, mit der er ausgehend von (m,k) sicher gewinnt. (m,k) heißt Verlustposition, wenn es für jeden Zug, den der Spieler am Zuge machen kann, eine Strategie seines Gegners gibt, mit der dieser sicher gewinnt.
1. Geben Sie eine Gewinnstrategie für dieses Spiel an.
2. Welches N sollten A bzw. B wählen, um ihre Gewinnchancen zu maximieren? Gibt es ein "faires N"?
Ein Rückgriff auf allgemeine Prinzipien der Spieltheorie ist nicht erforderlich, um dieses Problem zu lösen. Es kann aber nützlich sein, das Spiel "Würfel-Nim" in einen allgemeineren Zusammenhang zu stellen. Würfel-Nim ist ein endliches Zweipersonenspiel. Solche Spiele lassen sich mit speziellen Graphen darstellen, nämlich mit Bäumen, die alle denkbaren Spielverläufe abbilden. Jeder Knoten stellt die Ausgangslage für den jeweiligen Spieler am Zug dar, bevor er seinen Zug ausführt. Jede Kante im Baum stellt einen möglichen Zug dar, der Knoten darunter also die neue Ausgangslage (für den Gegner) nach diesem Zug. Von einem Knoten gehen also immer so viele Kanten (nach unten) aus, wie es Zugmöglichkeiten für den Spieler am Zuge gibt. Die untersten Knoten stellen Spielstände dar, die das Spiel beenden oder für die der Ausgang des Spiels klar ist. Natürlich wird es bei den meisten Spielen mit solchen Baumstrukturen mehrere verschiedene Knoten mit denselben Spielständen geben, da ein bestimmter Spielstand in der Regel mit verschiedenen Zugfolgen erreicht werden kann. (Bei Würfel-Nim steht der oberste Knoten für die Anfangssituation (n,j) und jeder andere Knoten für eine Position (m,k) ; auch hier gilt: ein bestimmtes (m,k) kann in mehreren Knoten vorkommen.) Die folgenden Bilder zeigen ein einfaches fiktives Spiel, das kein Unentschieden zulässt. Die linke Darstellung ordnet jede Ebene im Baum einem Spieler zu (schwarze Knoten für A am Zug, weiße Knoten für B am Zug). Die rechte Darstellung zeigt die Gewinn- und Verlustpositionen (grün für Gewinn, rot für Verlust), allerdings nur für die Endknoten.
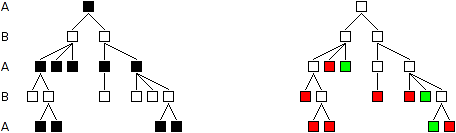
Für jedes halbwegs interessante Spiel sind diese Bäume zu groß, um sie vollständig durchrechnen zu können. Aber sie vermitteln durch ihre Struktur wesentliche Einsichten. Im rechten Bild sind absichtlich nur die Endknoten gefärbt worden. Denn dadurch sind alle anderen Knoten als Gewinn- oder Verlustpositionen determiniert. Insbesondere folgt aus den Endknoten die Färbung des obersten Knotens, also ob A oder B dieses Spiel gewinnt (fehlerloses Spiel vorausgesetzt). Eine kleine Vor-Übung für das Würfel-Nim-Problem: Welche Färbung haben die anderen Knoten im rechten Bild? Welche einfache Regel kann man dafür angeben? Gewinnt A oder B? Welche Zugfolge muss der Gewinner wählen? Diese Graphen zeigen also auf einfache Weise, dass die zugehörigen Spiele immer eine Optimalstrategie haben, dass also von vornherein festliegt, ob der Anziehende gewinnt oder der Nachziehende (falls beide keine Fehler machen). Eine Zusatzfrage: Was ändert sich an den Färbungsregeln für die Knoten, wenn das Spiel auch unentschieden enden kann?
Für Würfel-Nim lässt sich jeder Knoten durch das Zahlenpaar (m,k) beschreiben. Eine vollständige Analyse des Spiels kann man "von Hand" durchführen, allerdings erleichtert man sich durch ein kleines Programm die Arbeit. Welche besondere Gestalt hat der Baum für Würfel-Nim? Natürlich muss der Baum nicht vollständig durchlaufen werden, da sich die möglichen Spielstände jeweils in vielen Knoten finden. Aus der Struktur des Graphen benötigt man lediglich, durch welche Züge Knoten mit ihren Unterknoten zusammenhängen und auf welche Weise sich Gewinn- und Verlustpositionen aus den Unterknoten ergeben. Dann arbeitet man sich ausgehend von den Endknoten systematisch aufwärts durch die möglichen Spielstände.
Lösung
Wir wollen zuerst die theoretischen Fragen aus dem letzten Teil der Aufgabenstellung beantworten.
Die Färbungsregel für Bäume, die zu Spielen ohne Unentschieden gehören, lautet:
- Knoten ist Gewinnposition <--> mindestens ein Unterknoten ist Verlustposition
- Knoten ist Verlustposition <--> alle Unterknoten sind Gewinnpositionen
Dies gilt natürlich nicht für die Endknoten, die ja keine Unterknoten haben.
Das folgende linke Bild zeigt die vollständige Färbung für das Beispiel aus der Problemstellung. Es gibt nur zwei Wege durch den Baum, wenn beide Spieler fehlerfrei spielen (rechtes Bild). Also gewinnt A, wenn er die optimale Strategie befolgt.
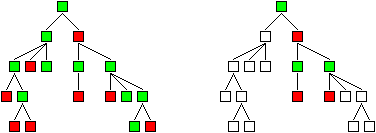
Was ändert sich an den bisherigen Überlegungen, wenn das Spiel auch Unentschieden zulässt?
- Knoten ist Gewinnposition <--> mindestens ein Unterknoten ist Verlustposition
- Knoten ist unentschiedene Position <--> kein Unterknoten ist Verlustposition, mindestens ein Unterknoten ist unentschiedene Position
- Knoten ist Verlustposition <--> alle Unterknoten sind Gewinnpositionen
In der folgenden Skizze sieht man ein Beispiel für ein Spiel, dass auch Unentschieden enden kann. Gelbe Knoten stehen für unentschiedene Positionen. Links sind nur die Endknoten eingefärbt. Die obigen Regeln ermöglichen die Färbung aller Knoten (mittleres Bild). Rechts sieht man die einzigen zwei Wege durch den Baum, wenn beide Spieler fehlerfrei spielen (das Spiel endet dann unentschieden).
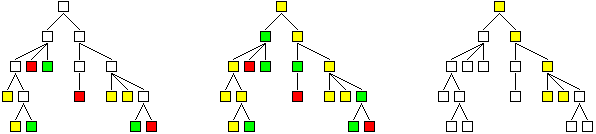
Welche besondere Gestalt hat der Baum für Würfel-Nim?
Der Baum für Würfel-Nim hat eine durchgehend einheitliche Gestalt: Jeder Knoten (außer den Endknoten) hat genau vier Unterknoten, denn der Würfel kann bei jedem Zug auf vier verschiedene Seiten gedreht werden. Dass sich die Anzahl der Knoten von einer Ebene zur nächsten vervierfacht, sollte aber nicht abschreckend wirken. Denn wie schon in der Aufgabenstellung dargestellt, müssen ja nicht alle Knoten, sondern nur alle verschiedenen Spielstände (m,k) analysiert werden.
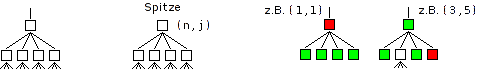
In der zweiten dieser vier Grafiken ist j die vor Beginn des Spiels gewürfelte Augenzahl. Die beiden rechten Grafiken zeigen beispielhaft, wie Endknoten entstehen können: Entweder zu viert nebeneinander oder zusammen mit mindestens einem Knoten, der weitere Unterknoten hat.
Es ist naheliegend, als Endknoten die Positionen mit m ≤ 0 zu nehmen. Die Endknoten mit m < 0 sind trivial (Gewinnpositionen). Die Endknoten (0,k) sind Verlustpositionen; es bietet sich an, die Analyse mit ihnen zu beginnen. Die nächsten Schritte sind sinnvollerweise (1,k) , dann (2,k) usw. Bei jedem dieser Spielstände führen die vier möglichen Züge auf bereits bekannte Spielstände. Durch Probieren oder durch ein Programm erkennt man schnell, dass es wesentlich mehr Gewinn- als Verlustpositionen gibt. Daher ist es einfacher, nur die Verlustpositionen aufzulisten. Diese Darstellung ist auch günstiger für die Spieler, denn sie werden immer versuchen, durch ihren Zug eine Verlustposition zu hinterlassen.
Also ans Werk: Ist m = 1 , so wird der Spieler am Zuge den Würfel auf k = 1 drehen wollen, da er in jedem anderen Falle verlieren würde. Diese Drehung kann er aber nicht ausführen, wenn er k = 1 oder k = 6 vorfindet. Also notieren wir als erste Verlustpositionen: (1,1), (1,6) . m = 2 ist dagegen immer eine Gewinnposition, denn eine Drehung auf k = 2 oder k = 1 ist immer möglich (hinterlässt für den Gegner die Verlustposition (0,2) bzw. (1,1)). Ist m = 3 , so wird der Spieler am Zuge den Würfel auf k = 3 drehen wollen, da er in jedem anderen Falle verlieren würde. Diese Drehung kann er aber nicht ausführen, wenn er k = 3 oder k = 4 vorfindet. Wir haben also zwei weitere Verlustpositionen gefunden: (3,3), (3,4) . Der Zusammenhang dieser Überlegungen mit der Baumstruktur soll anhand (m,k) = (3,5) deutlich gemacht werden:
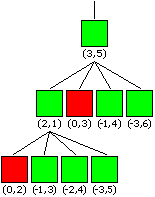
Auf diese Weise arbeitet man sich aufwärts, bis man ein Muster erkennt. Hier sind die Verlustpositionen:
(0,1) (0,2) (0,3) (0,4) (0,5) (0,6)
(1,1) (1,6)
(3,3) (3,4)
(4,3) (4,4)
(5,2) (5,5)
(8,3) (8,4)
(9,1) (9,2) (9,3) (9,4) (9,5) (9,6)
(12,3) (12,4)
(13,3) (13,4)
(14,2) (14,5)
(17,3) (17,4)
(18,1) (18,2) (18,3) (18,4) (18,5) (18,6)
(21,3) (21,4)
(22,3) (22,4)
(23,2) (23,5)
(26,3) (26,4)
(27,1) (27,2) (27,3) (27,4) (27,5) (27,6)
Offenbar gibt es eine Wiederholung in Neunergruppen. Folgende Regelmäßigkeiten scheinen aufzutreten:
- Ist m ein Vielfaches von 9 , so ist (m,k) immer eine Verlustposition.
- Ist m mod 9 gleich 1, 2, 6 oder 7 , so ist (m,k) immer eine Gewinnposition.
Einzige Ausnahmen: (1,1) und (1,6) sind Verlustpositionen.
- Ist m mod 9 gleich 3, 4 oder 8 , so sind nur (m,3) und (m,4) Verlustpositionen.
- Ist m mod 9 = 5 , so sind nur (m,2) und (m,5) Verlustpositionen.
Falls sich diese Regelmäßigkeit beweisen lässt, haben wir einen einfache und vollständige Darstellung aller Verlustpositionen gefunden. Der induktive Beweis enthält gleichzeitig die optimale Strategie, denn für jedes (m,k) wird der beste Zug angegeben.
Die vier Regeln wurden bereits bis m = 27 ausprobiert. Die Induktionsannahme sei nun, dass sie für alle m ≤ 9i gelten. Es ist dann 9i + 1 ≤ m ≤ 9(i+1) zu überprüfen; dies entspricht der Modulo-Schreibweise in der linken Spalte der folgenden Tabelle.
| |
Gewinnzug
Würfel drehen auf: |
Ausnahmen |
| m mod 9 = 1 |
1 oder 5 |
i = 0 : drehen auf 1, falls möglich |
| m mod 9 = 2 |
2 oder 3 |
i = 0 : drehen auf 1 oder 2 |
| m mod 9 = 3 |
3 oder 4, falls möglich |
i = 0 : drehen auf 3, falls möglich |
| m mod 9 = 4 |
4, falls möglich |
|
| m mod 9 = 5 |
5, falls möglich |
|
| m mod 9 = 6 |
3 oder 6 |
|
| m mod 9 = 7 |
2, 3 oder 4 |
|
| m mod 9 = 8 |
4, falls möglich |
|
| m mod 9 = 0 |
- |
|
Die Angaben in der Tabelle lassen sich leicht überprüfen (für die ersten Zeilen mit Hilfe der Induktionsannahme); damit ist der Beweis erbracht.
Während des Spiels reicht es, die Verlustpositionen zu kennen und nach Möglichkeit seinem Gegner zu hinterlassen. Man kann sie sich in einer übersichtlichen Form merken:
( 9·i , · )
( 9·i + 3 , 3 und 4 )
..4
..8
( 9·i + 5 , 2 und 5 )
( 1 , 1 )
( 1 , 6 )
Die folgende Graphik zeigt für m > 1 Gewinnpositionen in grün und Verlustpositionen in rot.
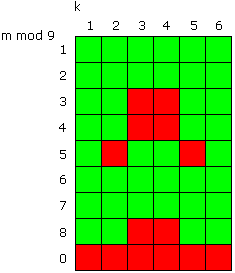
Gewinnaussichten für A und B
Eine Überlegung vorab: Würde n direkt gewählt (ohne vorherige Subtraktion einer gewürfelten Zahl), so würde A ein n wählen mit n mod 9 = 1, 2, 6 oder 7 , und B ein n mit n mod 9 = 0 , mit jeweils sicherem Gewinn. Eine Bestimmung von n durch Zufallszahlen würde nach der obigen Analyse der Verlustpositonen A in ca. 74,1 % aller Spiele gewinnen lassen (14 Verlustpositionen unter 54 möglichen Positionen), immer strategisch korrektes Spiel vorausgesetzt.
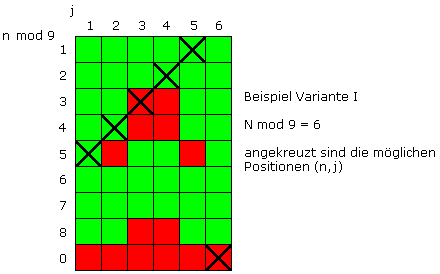
In der obigen Graphik der Gewinn- und Verlustpositionen setzen wir nun m = n und k = j , um die Gewinnaussichten für A und B in Abhängigkeit der beiden Varianten zu berechnen. Das nächste Bild zeigt beispielhaft, wie man vorgeht. Ist N mod 9 = 6 , so nimmt n mod 9 einen Wert zwischen 0 und 5 an, da die Augenzahl j von N subtrahiert wird. Bei Variante I kommen dann die angekreuzten Felder als Ausgangspositionen in Frage, und man sieht, dass die Gewinnwahrscheinlichkeit für A 2/3 beträgt.
Hier ist die vollständige Liste für Variante I:
Gewählt wird
N mod 9 = Gewinnw'keit für A
1 4/6
2 4/6
3 4/6
4 5/6
5 5/6
6 4/6
7 3/6
8 5/6
0 6/6
Es folgt ein Bild für ein Beispiel nach Variante II:
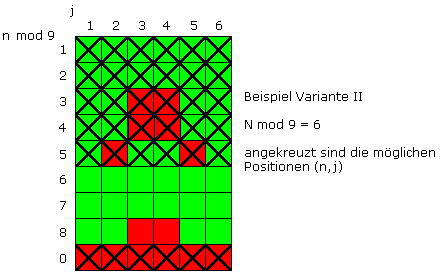
Hier ist die vollständige Liste für Variante II:
Gewählt wird
N mod 9 = Gewinnw'keit für A
1 24/36
2 26/36
3 28/36
4 26/36
5 24/36
6 24/36
7 30/36
8 30/36
0 28/36
Zusammenfassung der Gewinnwahrscheinlichkeiten für A bei optimalem Verhalten von A bzw. B:
| |
Variante I |
Variante II |
| |
N mod 9
W'keit |
N mod 9
W'keit |
| A wählt N |
0
100 % |
7 oder 8
83,3 % |
| B wählt N |
7
50 % |
1, 5 oder 6
66,7 % |
Es gibt also "faire N", nämlich alle N mit N mod 9 = 7 in Variante I (z.B. N = 34 oder N = 43 ). Demnach ist es beim Würfel-Nim zu bevorzugen, dass Variante I gespielt wird und B die Zahl N wählen darf.
Publiziert 2007-03-12 Stand 2006-06-09
voriges Problem |
Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite