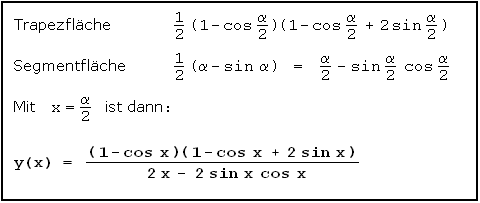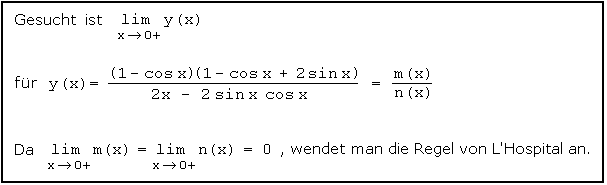Die chinesische Trapezregel für Kreissegmente aus "Mathematik in neun Büchern"

          Die Lösung steht im unteren Teil der Seite.

Gleichzeitig mit diesem Problem wird eine Briefmarkenseite publiziert, die dem chinesischen Mathematiker Liu Hui aus dem 3. Jahrhundert gewidmet ist. Dieser hat einen Kommentar zu dem noch älteren Werk "Mathematik in neun Büchern" geschrieben. Darin wird angegeben, wie man den Flächeninhalt eines Kreissegments näherungsweise durch den Flächeninhalt eines Trapezes berechnen kann, und zwar wie in der folgenden Skizze:



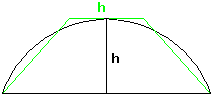
Bild 1

In Worten lautet diese Regel:

Segmentfläche ≈ Höhe·(Höhe + Sehne)/ 2

Segment und Trapez haben also die gleiche Höhe, die Basis des Trapezes ist die Sehne des Segmentes, und die Parallelseite und die Höhe des Trapezes sind gleich lang.

Überprüft man die Flächeninhalte von Segment und Trapez, so stellt man fest, dass die Näherung nicht besonders gut ist. Für den Spezialfall, dass das Segment ein Halbkreis mit Radius  r  ist, gibt Liu Hui die Trapezfläche mit  ³/₂ · r²  an (siehe Briefmarkenseite); diese Approximation der Segmentfläche unterschätzt den wahren Wert um ca.  5 %  oder genauer um  (1 - 3/π)·100 % . Außerdem schreibt Liu Hui, dass die Approximation der Segmentfläche durch die Trapezfläche für kleinere Segmente schlechter wird.

Wir betrachten der Einfachheit halber einen Kreis mit Radius  1 . Die Höhe  h  eines Segmentes bewegt sich im Intervall (0,1] , der zugehörige Mittelpunktswinkel  α  im Intervall (0,π] , siehe Bild 2.


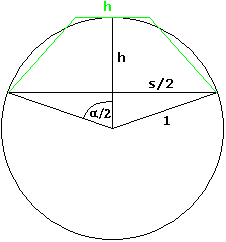
Bild 2

Auf den ersten Blick sieht das folgende Problem nicht allzu schwierig aus:

(1)  Wie hängt das Verhältnis der Flächeninhalte von Segment und Trapez (und damit der Fehler bei der Approximation) von der Größe des Segments ab, also von  h  bzw.  α ?

Natürlich lässt sich dafür leicht eine Formel aufstellen. Damit kann man auch Liu Huis Ergebnis für den Halbkreis überprüfen. Aber sofort stellen sich Fragen ein:

(2)  Kann man Liu Huis Aussage so verstehen, dass das Verhältnis der Flächeninhalte monoton fällt, wenn  h  bzw.  α  kleiner werden? Das würde bedeuten: Der Approximationsfehler wächst, wenn das Segment kleiner wird.

(3)  Wie groß ist der Grenzwert für das Verhältnis der Flächeninhalte für  h → 0  bzw.  α → 0 ?

Die Fragen (2) und (3) kann man empirisch mit Rechnerunterstützung lösen. Will man sie streng mathematisch behandeln, laufen sie auf eine Kurvendiskussion hinaus. Dafür kenne ich keinen wirklich einfachen Weg, aber vielleicht findet einer der Leser dieser Seite einen solchen; über eine entsprechende Mitteilung wäre ich sehr erfreut.

Ich will ein paar Hinweise geben und den Beweisweg, den ich selbst gegangen bin, grob skizzieren. In Bild 2 sind die relevanten Größen eingetragen. Für meinen Geschmack ist die Funktion  y , die es zu diskutieren gilt, einfacher in Abhängigkeit von  α  (noch besser  x = α/2 ) als von  h  zu untersuchen.  y(x)  ist dann also der Quotient der Flächeninhalte von Trapez und Segment; beide lassen sich leicht durch  x = α/2  ausdrücken.

An dieser Stelle wird man gerne ein Computeralgebra-Programm oder einen guten Graphik-Taschenrechner hinzuziehen, um sich ein erstes Bild von  Graph(y)  zu machen. Und tatsächlich:  y  wächst streng monoton gegen  3/π , wenn  x  das Intervall (0,π/2]  durchläuft, und der Grenzwert bei  0  scheint nahe bei  0.75  zu liegen. Also haben wir bereits eine erste Antwort auf die Fragen (2) und (3), nämlich: Wird das Segment immer kleiner (ausgehend vom Halbkreis), so steigt der Approximationsfehler streng monoton von ca.  5 %  auf ca.  25 % .

Wie kann man dies nun mathematisch untermauern? Ich denke, es ist legitim, sich bei den benötigten Ableitungen von einem Rechner helfen zu lassen, um nicht die Lust zu verlieren. Für (3) gibt es eine Standardmethode aus der Analysis, die in unserem Problem eine sehr schöne Anwendung findet. (2) ist aufwändiger, obwohl nur  y' > 0  gezeigt werden muss. Bei der Analyse von  y' sollte man den Rechner die Routinearbeit machen lassen. Man benötigt höhere Ableitungen und sollte bei jedem Schritt verschiedene Termsortierungen ausprobieren. Ein letzter Tipp: Ich habe das Definitionsintervall halbiert und die beiden Hälften getrennt untersucht.

Lösung

Zu (1)

Wir berechnen zunächst  y . Die Segmentfläche kann man in einer Formelsammlung nachschauen, aber wir wollen sie mit Hilfe der folgenden Beziehungen herleiten (siehe Bild 2):

Die Fläche des zugehörigen Kreissektors verhält sich zur Kreisfläche ( = π ) wie  α  zu  2π  und ist somit gleich  α/2 . Davon ist die Dreieckfläche mit Basis  s = 2·sin α/2  und Höhe  1 - h = cos α/2  zu subtrahieren, also  cos α/2 · sin α/2 = ¹/₂·sin α . Die Trapezfläche ist  h·(h+s)/2 . Nun können wir  y  als Funktion von  α/2  ausdrücken:



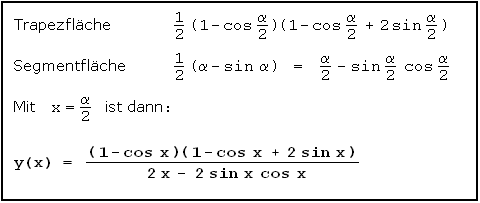
Damit kann man  Graph y  zeichnen:



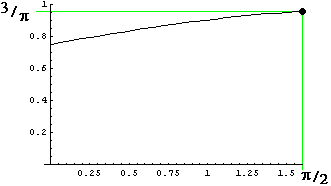
Graph y

Wie schon in der Aufgabenstellung angegeben, wächst  y  offenbar streng monoton gegen  3/π ; der Grenzwert für  x → 0  liegt nahe bei  0.75 . Im folgenden werden wir diese Kurve aber auch "von rechts nach links lesen", wenn wir beim Halbkreis beginnen und dann das Segment schrumpfen lassen: Das Verhältnis von Trapez- zu Segmentfläche fällt dann monoton, und der Approximationsfehler wächst.


Zu (2)

y'  kann man mit etwas Geduld von Hand ausrechnen:



Farbig unterlegt ist das MATHEMATICA-Ergebnis dargestellt. Wenn man von Hand rechnet, ist das Ausklammern von  1 - cos x  (entspricht  2·Sin[x/2]²  im MATHEMATICA-Ergebnis) ziemlich wichtig, weil sich dadurch das Problem sehr vereinfacht. Der Bruch als Vorfaktor ist nämlich positiv, so dass nur noch untersucht werden muss, ob der Klammerausdruck positiv ist. Für dessen Analyse habe ich bis zur 4. Ableitung gerechnet:

Ab der zweiten Ableitung von  z  wurden immer  sin x  und  cos x  ausgeklammert und dann untersucht, ob die Klammerausdrücke positiv sind. (Natürlich kommen auch andere Sortierungen der Terme in Betracht, die möglicherweise den Beweis vereinfachen.) Für  x ≤ π/4  reicht die 2. Ableitung, für  x > π/4  habe ich die 4. Ableitung benutzt.

1. Fall
0 < x ≤ π/4

   Erste innere Klammer von  z''(x) :
   g(x) = sin x + cos x - 1 - x/2
   g''(x) = - sin x - cos x < 0
   g  ist also konkav. Wegen  g(0) = 0  und  g(π/4) > 0  folgt  g(x) > 0 .

   Zweite innere Klammer von  z''(x) :
   h(x) = 1 - x + sin x - cos x
   h'(x) = -1 + cos x + sin x > 0  und  h(0) = 0  ⇒  h(x) > 0

   Also ist  z''(x) > 0 . Wegen  z'(0) = 0  ist dann  z'(x) > 0 ,
   und wegen  z(0) = 0  ist auch  z(x) > 0 .

2. Fall
π/4 < x ≤ π/2

   Erste innere Klammer von  z⁽⁴⁾(x) :
   6 + x - 8 sin x - 8 cos x < 0  wegen  6 + x < 8  und  -8 sin x - 8 cos x ≤ -8 .

   Zweite innere Klammer von  z⁽⁴⁾(x) :
   -4 + 2x - 8 sin x + 8 cos x < 0  wegen  -4 + 2x < 0  und  cos x - sin x < 0 .

   Also ist  z⁽⁴⁾(x) < 0 .
   ⇒   Wegen  z'''(π/4) < 0  ist  z'''(x) < 0 .
   ⇒   Wegen  z''(π/4) > 0   und  z''(π/2) < 0  hat  z''  genau eine Nullstelle.
   ⇒  z'  wächst monoton bis zu einem Maximum und fällt dann monoton;
      wegen  z'(π/4) > 0  und  z'(π/2) < 0  hat  z'  genau eine Nullstelle
   ⇒  z  wächst monoton bis zu einem Maximum und fällt dann monoton;
      wegen  z(π/4) > 0   und  z(π/2) > 0  ist  z(x) > 0 .

Insgesamt haben wir also erhalten:  z(x) > 0  und damit  y'(x) > 0  für  0 < x ≤ π/2   ⇒   y  wächst streng monoton.


Zu (3)



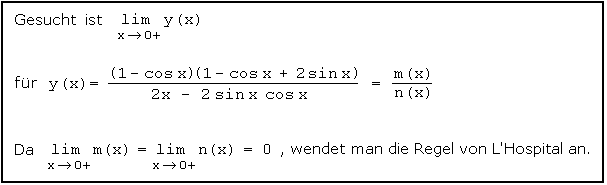
Gemäß der Regel von L'Hospital setzt man im Grenzwert von  y(x)  für  m(x)  und  n(x)  jeweils deren Ableitungen  m'(x)  und  n'(x)  ein, was zum selben Ergebnis führt. Wie wir im nächsten Kasten sehen, muss man diesen Vorgang geduldig wiederholen:




Lässt man also das Kreissegment vom Halbkreis beginnend schrumpfen, so fällt das Verhältnis von Trapezfläche zu Segmentfläche monoton von  3/π  auf  3/4 .

Dies ist ein bemerkenswert schönes Beispiel für den Einsatz der L'Hospital'schen Regel. Dass man bei einem realen Anwendungsproblem die Regel gleich dreimal in Folge verwenden muss, ist wohl eher selten.



Kategorie: Chinesische Mathematik

Publiziert 2006-12-14          Stand 2006-04-15

voriges Problem   |    Liste aller Probleme mit Lösungen   |    nächstes Problem