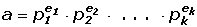Briefmarke des Monats Februar 2005
 |
DDR 1981
Michel 2605
Scott 2181
|
Richard Dedekind (1831 - 1916)
Richard Dedekind stammte aus Braunschweig und studierte Mathematik an der Universität Göttingen. Er war der letzte Doktorand von Carl Friedrich Gauß. Ab 1858 arbeitete er als Professor am Polytechnikum Zürich, ab 1862 am Polytechnikum Braunschweig. - Die Briefmarke wurde anlässlich seines 150. Geburtstages ausgegeben.
Dedekind leistete bedeutende Beiträge zu Grundlagenproblemen der Mathematik (Begriff der Zahl, Begriff der Menge, Begriff des Unendlichen), zur Differential- und Integralrechnung, zur Zahlentheorie und zur Algebra. Für seine Untersuchungen der algebraischen Zahlkörper führte er das Konzept des Ideals ein. Die Formel auf der Briefmarke entstammt der Idealtheorie und wird weiter unten erklärt.
Dedekinds Name taucht auch bei der Konstruktion der reellen Zahlen aus den rationalen Zahlen Q auf. Eine reelle Zahl lässt sich als Dedekind'scher Schnitt definieren. Ein solcher Schnitt ist eine Partition der rationalen Zahlen in zwei disjunkte Teilmengen A und B , wobei jedes Element von A kleiner als jedes Element von B ist. Ein einfaches Beispiel: Die Quadratwurzel von 3 ist nach Dedekinds Ansatz definiert durch
A = { x | x rational, x2 < 3 } , B = Q \ A .
Die Formel auf der Briefmarke sieht aus wie die Primfaktorzerlegung einer natürlichen Zahl, z.B. 38808 = 23·32·72·11 . Aber dies war lange vor Dedekind bekannt. Hier bedeutet die Formel eine Verallgemeinerung innerhalb der allgemeinen Algebra, die von Dedekind in die Ringtheorie eingeführt wurde.
Dedekind befasste sich mit der Frage, in welchen anderen Zahlbereichen eine eindeutige Primfaktorzerlegung möglich ist. Betrachten wir zunächst die Menge Z der ganzen Zahlen. Die Primzahlen in Z sind die natürlichen Primzahlen und ihre Negativen. Die Eindeutigkeit der Zerlegung gilt dann streng genommen nicht, da z.B. -6 = 2·(-3) = (-2)·3 gilt und 2, 3, -2, -3 sämtlich prim sind. Die Eindeutigkeit lässt sich aber durch eine Modifikation retten. Dazu soll das Konzept der Primzahl in einem abstrakten Rahmen betrachtet werden, im Hinblick auf Dedekinds Werk. Man bezeichnet Elemente, zu denen ein multiplikativ inverses Element existiert, als Einheiten; Z hat dann nur die Einheiten 1 und -1 . Eine Nicht-Einheit q soll irreduzibel heißen, wenn aus q = n·m folgt, dass n oder m eine Einheit ist. Eine Nicht-Einheit p soll prim heißen, wenn aus " p teilt n·m " folgt " p teilt n oder m " . In Z stimmen die irreduziblen Zahlen mit den Primzahlen überein.
Zurück zur Zerlegung in Primfaktoren: Jedes Element von Z (außer 0, 1, -1 ) hat eine Primfaktorzerlegung, die bis auf die Multiplikation der Faktoren mit Einheiten eindeutig ist. Dies soll nun im allgemeineren Rahmen der Ringtheorie betrachtet werden: Z ist ein faktorieller Ring, d.h. eine Menge mit:
- kommutativer und assoziativer Addition mit Null und inversen Elementen
- kommutativer und assoziativer Multiplikation mit Eins
- Distributivgesetz
bis hier: "Kommutativer Ring mit Eins"
- Eins und Null sind verschieden.
- Nullteilerfreiheit: Aus n·m = 0 folgt n = 0 oder m = 0 .
d.h. "Integritätsring"
- Faktorisierbarkeit: Jedes Element außer den Einheiten und der Null hat eine Zerlegung in irreduzible Elemente, die bis auf die Multiplikation der Faktoren mit Einheiten eindeutig bestimmt ist.
In faktoriellen Ringen stimmen (wie in Z ) die irreduziblen Elemente und die Primelemente überein.
Dedekind untersuchte andere Ringe von Zahlen darauf, ob sie faktoriell sind. Wir wollen hier zwei Beispiele aus dem Bereich der Ringe ganzer Zahlen in imaginär-quadratischen Zahlkörpern betrachten.
Das erste Beispiel ist die Menge der Gauß'schen Zahlen Z[i] , bestehend aus den komplexen Zahlen n + m·i mit n, m ganzzahlig. Z[i] wird durch die Gitterpunkte mit ganzzahligen Koordinatenwerten in der komplexen Zahlenebene dargestellt. Z[i] ist ein faktorieller Ring mit den Einheiten 1, -1, i, -i . Während z.B. 3 eine Primzahl in Z[i] ist, gilt dies nicht für alle natürlichen Primzahlen: Es ist z.B. 2 = (1+i)·(1-i) und 5 = (2+i)·(2-i) , also sind 2 und 5 nicht prim in Z[i] . Die Faktoren 1 ± i und 2 ± i sind Primzahlen, also haben wir für 2 und 5 die eindeutige Primfaktorzerlegung angegeben. Diese gilt aber nur bis auf die Multiplikation der Faktoren mit Einheiten; es gilt auch 5 = (-1+2i)·(-1-2i) .
Das zweite Beispiel ist Z[d] ; hier soll d für i·√5 stehen. Z[d] besteht aus allen Zahlen n + m·i·√5 mit n, m ganzzahlig und wird ebenfalls durch ein Gitter in der komplexen Zahlenebene dargestellt; 1 und -1 sind die einzigen Einheiten. Auch in Z[d] lassen sich die Zahlen irreduzibel faktorisieren, aber hier gilt nicht mehr die Eindeutigkeit. So ist z.B. 6 = 2·3 = (1+d)·(1-d) . Alle vier Faktoren sind irreduzibel, aber nicht prim (z.B. teilt 2 das Produkt (1+d)·(1-d) , aber keinen der beiden Faktoren). Z[d] ist also kein faktorieller Ring.
Dedekind fand aber einen Weg, eindeutige Primfaktorzerlegungen auch für Z[d] (und andere Ringe ganzer Zahlen) zu ermöglichen, allerdings nicht für Zahlen, sondern für Ideale. Ein Ideal ist eine Teilmenge eines Rings, bei der die Summe zweier Idealelemente und das Produkt eines Idealelements mit einem beliebigen Ringelement wieder im Ideal liegen. Echte Ideale sind von {0} und vom Ring verschieden. In Z bildet die Teilmenge der geraden Zahlen oder allgemeiner der durch ein natürliches n teilbaren Zahlen jeweils ein Ideal, nicht jedoch die ungeraden Zahlen. Ein Produkt von Idealen a1 ... ak besteht aus allen endlichen Summen von Produkten x1 · ... · xk mit xi aus ai . Mit a = <x1 ... xn> wird das Ideal bezeichnet, das von den Elementen x1 ... xn "erzeugt" wird; es besteht aus allen Linearkombinationen b1x1 + ... + bnxn mit Ringelementen bi . Ein Ideal p heißt Primideal, wenn aus x1·x2 in p folgt, dass x1 oder x2 in p liegt. In Z und Z[i] sind die Primideale genau die durch jeweils eine Primzahl erzeugten Ideale. Mit dieser Begriffsbildung gilt der auf Richard Dedekind zurückgehende Satz, dessen Hauptformel auf der Marke abgebildet ist:
In Z[d] (und anderen Ringen ganzer Zahlen in imaginär-quadratischen Zahlkörpern) lässt sich jedes echte Ideal a eindeutig als endliches Produkt von Primidealen pi darstellen:
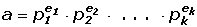
Beispiel für Z :
<30> = <2>·<3>·<5>
120 liegt in <30> und hat die Primfaktorzerlegung 23·3·5 = (4·2)·3·5 mit 4·2 in <2> .
Beispiel für Z[i] :
<6> = <3>·<1+i>·<1-i>
-12 liegt in <6> und hat die Primfaktorzerlegung 3·(1+i)·(-1+i) mit -1+i in <1-i> .
Beispiel für Z[d] :
<6> = <2,1+d>2·<3,1+d>·<3,1-d>
Da Z[d] nicht faktoriell ist, gibt es hier im allgemeinen keine eindeutige Zerlegung in Ideale, die nur von einer einzigen Zahl erzeugt werden (Hauptideale). Die drei Ideale auf der rechten Seite lassen sich als Primideale nachweisen. Das vierfache Idealprodukt ist die eindeutige Zerlegung von <6> in Primideale.
Wie lässt sich nun konkret die Zahl 6 als Element des Primidealprodukts darstellen? (Daraus folgt dann die entsprechende Darstellung aller Vielfachen (n + m·d)·6 .)
Erster Schritt: Man schreibt 6 = 2·3 und stellt die Faktoren als 2 = 6-4 und 3 = 9-6 dar.
Zweiter Schritt: Wegen 6 = (1+d)·(2-(1+d)) und -4 = 2·(-2) liegen 6 und -4 in <2,1+d>2 . Wegen 9 = 3·3 und -6 = (1+d)·(-1+d) liegen 9 und -6 in <3,1+d>·<3,1-d> .
Dritter Schritt: Ausmultipliziert ist dann
6 = 2·3 = (6-4)·(9-6) = 6·9 + 6·(-6) + (-4)·9 + (-4)·(-6) = (1+d)·(2-(1+d))·3·3 + (1+d)·(2-(1+d))·(1+d)·(-1+d) + 2·(-2)·3·3 + 2·(-2)·(1+d)·(-1+d)
Jeder der letzten vier Summanden hat vier Faktoren, von denen die beiden ersten aus <2,1+d> stammen, die beiden letzten aus <3,1+d> bzw. <3,1-d> . Also liegt 6 in <2,1+d>2·<3,1+d>·<3,1-d>.
Kategorie: Zahlen und Zahlsysteme, Berechnung von π
Stand 2004-11-23
vorige Marke | Liste aller Briefmarken | nächste Marke | Mathematische Philatelie
Manfred Börgens | zur Leitseite