deutsche Version

Slovenia 1994

Jurij Vega (1754 - 1802)

Jurij Vega was a Slovenian mathematician und military engineer. At his lifetime, Slovenia belonged to the Austrian Habsburg empire; his German name was Georg Vega. Vega was trained as a navigational engineer, and until 1780, he worked with projects for river regulation. At the age of 26, he became a professional soldier in the imperial army. There he managed to display his technical and scientific interests and abilities: studies in mathematics, sciences, ballistics und geodesy, training as an artillery officer, appointment as a professor for mathematics at the military academy in Vienna, publication of several mathematical books and articles.

Jurij Vega was also a devoted soldier and fought in battles against the Turkish, French and Prussian armies. For his military merits he was raised to the peerage in 1800 with the title Georg Freiherr von Vega. Vega was murdered two years later under mysterious circumstances.

Vega became famous by two publications. From 1793 to 1797, he produced seven figure logarithm tables which were printed in 100 editions until 1957. These tables were devised for high precision artillery calculations, but soon their exactness and reliability were also appreciated for civil applications. Vegas second historical achievement was a world record in the calculation of  π : He calculated 136 correct decimal places; this record remained unbroken from 1794 to 1824. Vega used the arctangent power series:

arctan x = x - x³/3 + x⁵/5 - x⁷/7 + ...

The smaller  x , the faster this series converges. Vega used the arctangent series in two ways:

π = 20 arctan ¹/₇ + 8 arctan ³/₇₉
π = 8 arctan ¹/₃ + 4 arctan ¹/₇

π-formulae of this kind were well known in the 18th century. They go back to the tangent addition theorem:

tan (α +- β) = (tan α +- tan β) / (1 -+ tan α · tan β)

With  a = tan α  and  b = tan β  we get for  1 -+ a·b > 0 :

arctan a +- arctan b = arctan (a +- b)/(1 -+ a·b)

From this Vega's second formula for  π  follows:

a = 1 , b = ¹/₇    -->    ^π/₄ - arctan ¹/₇ = arctan ³/₄
a = b = ¹/₃        -->    2 arctan ¹/₃ = arctan ³/₄

The first formula for  π  can be deduced in a similar but more labourious way by multiple application of the arctangent addition theorems above. We describe here a different and more elegant way: For a complex number  u + i·v = e^iφ ,  φ = arg (u + i·v)  is the angle belonging to this number in the complex plane, counterclockwise oriented from the positive real axis. For  u > 0 ,  φ = arctan ^v/_u . Complex multiplication in particular means addition of the angles; from this we get

5 arctan ¹/₇ + 2 arctan ³/₇₉ = arg (7 + i)⁵·(79 + 3i)² = arg 78125000(1 + i) = arg (1 + i) = arctan 1 = ^π/₄


What does the stamp show?
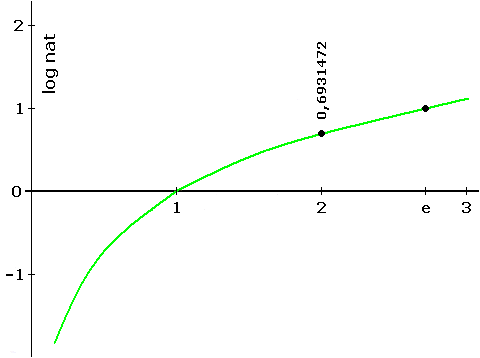
Above Vega's portrait, we see the logarithm curve and part of the surface of the moon which has a crater named "Vega".

Some details of the logarithm curve are difficult to make out on the stamp. The curve describes the natural logarithm to base  e . In the next sketch all details are reproduced. The vertical axis, missing on the stamp, has been included and the characteristic points  (1, 0), (2, 0.6931472)  and  (e, 1)  have been emphasized.




With the picture of the moon's surface, the stamp reminds us that a moon crater was named after Vega (45.4° south, 63.4° east, 76 km diameter). The designer also included the names of four other scientists who received the honour of a moon crater being named after them: Jean-Baptiste Biot (1774 - 1862), French mathematician und physicist; Dionysius Petavius (Denis Petau, 1583 - 1652), French Jesuit; Romana, Spanish Jesuit; William Parsons, Earl of Rosse (1800 - 1867), Irishman and builder of the biggest telescope of his time. In modern moon maps we sometimes find other names for some of these craters because many moon craters have been renamed during the 20th century.


The Slovenian 50 Tolar banknote also bears Jurij Vega's portrait, and shows a geometrical construction, a manifold of curves and the phases of the moon.