deutsche Version

Professor O.'s space flight

          Solution: See lower part of this page.

Professor O. goes on a space flight. He lands on a distant planet and gets a friendly welcome from the inhabitants. Soon they and their visitor manage to start a communication, and O. attends a mathematics lesson in a school. The teacher has written a calculation on the blackboard:



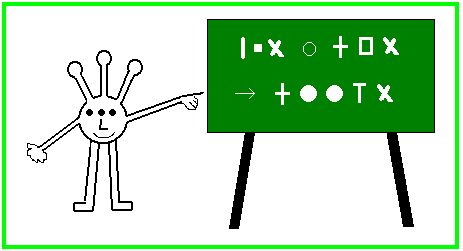
O. asks the teacher to explain the symbols in the calculation. Counting bars turns out to be the best intergalactic communication method. On the next blackboard you can see a few examples:



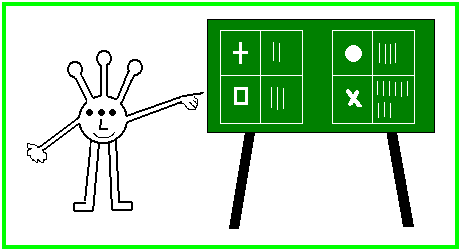
As soon as O. has understood all symbols in the calculation he writes down the calculation substituting the symbols by the familiar arabic numerals:



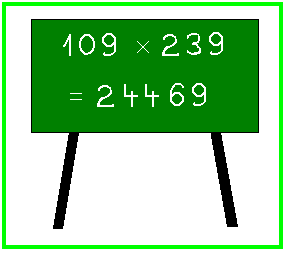
But the resulting equation seems strange to O. He sends a message to his colleague and number theory specialist Professor S. and asks him for his opinion. S. is a little bit mean and hides the solution behind the cryptic advice: "Count the fingers of your hosts." O. follows this advice. What will he discover?

Solution

Professor S. assumes that the aliens use a place value system for the representation of natural numbers  -  as we do  -  but with a base different from  10 . The number  239  on the third blackboard may serve as an example: It does not stand for  9 + 3·10 + 2·10²  but for  9 + 3·b + 2·b²  with an unknown base  b . (If S. is right then  b  is the number of fingers of O.'s hosts.) The calculation must then be interpreted as:

( 9 + b² )·( 9 + 3·b + 2·b² ) = 9 + 6·b + 4·b² + 4·b³ + 2·b⁴

In short:

b³ - 23·b² - 21·b - 72 = 0

This cubic equation is completely solvable  -  even by hand. But one need not determine all solutions. The easier way starts from the fact that there is (at least) one solution in the natural numbers (the number of fingers of the aliens). This number must divide the constant part of the cubic equation  ( -72 )  without remainder. The candidates are quickly checked  -  only one of them is a solution:  b = 24 . This is the only solution in the real numbers, the two other solutions are complex and not of interest for our problem.

With  b = 24  the multiplication on the blackboard can be translated to the decimal system:

585·1233 = 721305

How did S. deduce that the aliens write their numbers from left to right with descending powers  -  as we do  -  and not from right to left? He could not know but checked both ways. For ascending powers there is no natural solution.

Professor O. indeed counted  24  fingers on his hosts.