Wir betrachten zuerst den Fall von genau k Jungen in einer n-köpfigen Geschwisterschar. Die Relation (A,B) mit "B ist Schwester des Jungen A" besteht dann aus k(n-k) Paaren. k ist (n, 0.5)-binomialverteilt; die Werte dieser Verteilung sollen im Folgenden kurz mit b(k) abgekürzt werden. Wir erhalten so das gewichtete Mittel über die möglichen k :
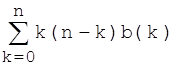
Dies ist also die durchschnittlich zu erwartende Anzahl der Paare (A,B) in den n-köpfigen Geschwisterscharen. Nun kommen aber in dieser Zahl alle Jungen unter den Geschwistern vor. Wir wollen die durchschnittliche Zahl von Schwestern für einen einzelnen Jungen berechnen und müssen deshalb noch durch die Anzahl der Jungen unter den Geschwistern dividieren; dies sind durchschnittlich n/2 . Wenn wir mit μ = n/2 den Erwartungswert und mit σ2 = n/4 die Varianz der (n, 0.5)-Binomialverteilung bezeichnen, erhalten wir:
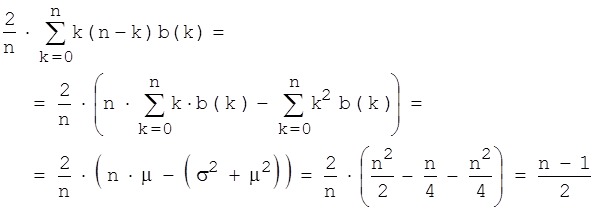
(n-1)/2 ist genau die Hälfte der Geschwister - das ist nicht wirklich überraschend. Nochmal zur Erläuterung der Rechnung: Für jeden einzelnen Jungen wird die Anzahl der Schwestern gezählt, dies ist n-k ; diese Anzahlen werden dann über alle k Jungen addiert, gewichtet mit der Wahrscheinlichkeit für die jeweilige Anzahl der Jungen in der Familie. n/2 ist die Anzahl der Jungen, durch die dividiert wird, so dass ein Durchschnitt über alle Jungen entsteht. k = 0 und k = n stehen für reine Mädchen- bzw. Jungen-Familien.
Wir rechnen das Gleiche nochmal für die Schwestern von k Mädchen. Für die Relation (A,B) mit "B ist Schwester des Mädchens A" gibt es dann k(k-1) Möglichkeiten. k ist wieder (n, 0.5)-binomialverteilt, so dass wir analog zu der Rechnung für die Jungen erhalten:
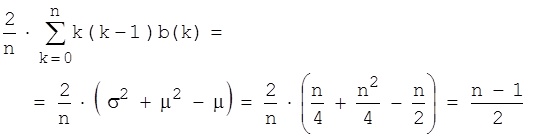
Jungen wie Mädchen haben also im Durchschnitt gleich viele, nämlich (n-1)/2 Schwestern.
Nun zur zweiten Frage.
Da die Anzahl der Kinder bei jeder Mutter biologisch nach oben begrenzt ist, wollen wir das folgende Modell betrachten: Ein Teil der Familien (die "Planer") entscheidet sich, nicht alles dem Zufall zu überlassen, sondern auf die Geburt des ersten Jungen zu warten und dann keine weiteren Kinder mehr zu bekommen. Einem Teil dieser Familien wird das nicht gelingen. Wir wollen deshalb eine Obergrenze m für die Anzahl der Kinder der "Planer" annehmen. In diesen Familien gibt es also so lange Nachwuchs, bis ein Junge geboren wird oder die Höchstzahl von m Kindern erreicht wird. Deshalb gibt es bei den "Planern", die genau m Kinder haben, sowohl welche mit genau einem Jungen als auch welche mit m Mädchen. - Das hier vorgestellte Modell mag etwas unrealistisch erscheinen, aber weiter unten wird gezeigt, dass es als Grundlage für ein allgemeineres und plausibleres Modell dient.
Es ist bekannt, dass keine Art der Familienplanung dazu führt, dass das 50%-50%-Verhältnis von Jungen und Mädchen in der Gesamtpopulation verändert wird. Aber man kann zeigen, dass die Frage nach der Anzahl der Schwestern sehr wohl vom Verhalten der Eltern abhängen kann. Dafür kann man viele Beispiele finden; hier wird ein naheliegendes betrachtet, nämlich das bereits beschriebene Verhalten der "Planer".
Anzahl der Schwestern eines Jungen (bei den "Planern"):
Da es jeder Familie maximal einen Jungen geben kann, wird hier die Argumentation leichter als bei der ersten Frage. Die Wahrscheinlichkeit, dass eine Mutter k Töchter und einen Sohn hat, ist 2-(k+1). Also ist die Wahrscheinlichkeit, dass ein Junge genau k Schwestern hat, die bedingte Wahrscheinlichkeit
p(k Töchter | 1 Sohn) = p(k Töchter ∧ 1 Sohn) / p(1 Sohn) = 2-(k+1)/(1-2-m)
Wir erhalten damit die durchschnittliche Anzahl von Schwestern für einen Jungen (bei den "Planern"):
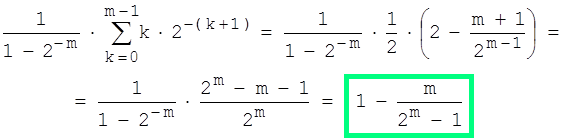
Die erste Gleichung bedarf einer Erklärung:
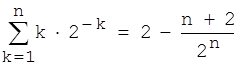
Begründung:
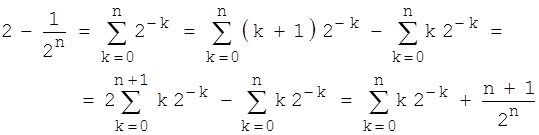
Anzahl der Schwestern eines Mädchens (bei den "Planern"):
Wir betrachten zuerst den Fall von genau k Mädchen in einer Familie, k = 0 ... m . Die Relation (A,B) mit "B ist Schwester des Mädchens A" besteht aus k(k-1) Paaren. k Mädchen in einer Familie kommen mit W'keit 2-(k+1) für k < m vor und mit W'keit 2-m für k = m . Wir erhalten so das gewichtete Mittel über die möglichen k :
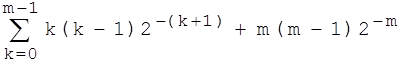
Dies ist also die durchschnittlich zu erwartende Anzahl der Paare (A,B) in einer Familie. Nun kommen aber in dieser Zahl alle Mädchen unter den Geschwistern vor. Da wir die durchschnittliche Zahl von Schwestern für ein einzelnes Mädchen berechnen wollen, müssen wir noch - wie beim ersten Problem - durch die Anzahl der Mädchen pro Familie dividieren; dies sind durchschnittlich die Hälfte aller Kinder, also
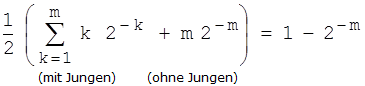
Wir wollen die beiden letzten Formeln zusammenführen. Dafür brauchen wir zunächst wieder eine Nebenrechnung:
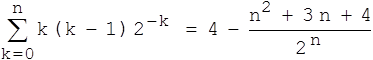
Begründung:
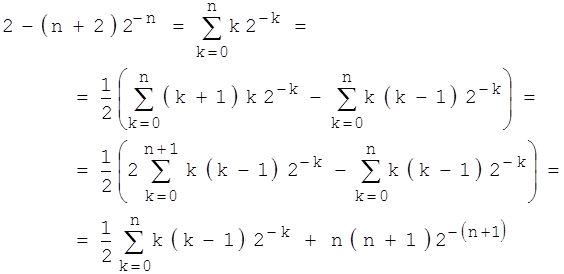
Also ist die durchschnittliche Anzahl von Schwestern für ein Mädchen (bei den "Planern"):
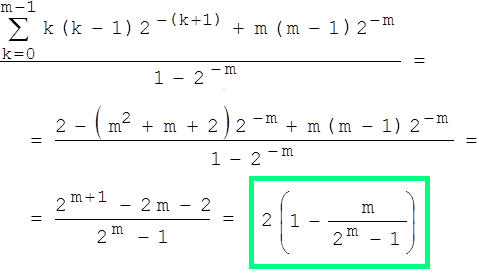
Das sind doppelt so viele wie bei den Jungen!
Beispiel: m = 7
Die Jungen in den "Planer"-Familien haben im Durchschnitt 120/127 ≈ 0,945 Schwestern.
Die Mädchen in den "Planer"-Familien haben im Durchschnitt 240/127 ≈ 1,89 Schwestern.
Nochmal der Hinweis: Die Aussage, dass keine Art von Familienplanung etwas an der zufälligen Zusammensetzung von Mädchen und Jungen zu ändern vermag, ist irreführend. Dies gilt zwar für den Anteil von Jungen und Mädchen pro Familie, aber nicht für alle Fragestellungen bzgl. Geschwistern - wie wir gerade bewiesen haben.
Nun ist es in der Tat etwas weltfremd, dass sich die "Planer" auf eine Kinderzahl m einigen und es dann auch allen "Planern" möglich ist, ggfs. bis zum m-ten Kind zu warten. Aber das spielt für unsere Argumentation nicht wirklich eine Rolle. Man kann sich vorstellen, dass die Gruppe der "Planer" in Untergruppen mit verschiedenen m zerfällt. Nimmt man beispielhaft die Untergruppe mit m = 4 , so handelt es sich um alle Familien, die sich vorgenommen hatten, nach dem ersten Sohn keine weiteren Kinder zu bekommen, die aber - aus welchen Gründen (z.B. Altersgründen) auch immer - nicht mehr als 4 Kinder bekommen können. - Für jede dieser Untergruppen mit m > 1 gilt nach unseren Berechnungen, dass die Mädchen mehr Schwestern haben als die Jungen.