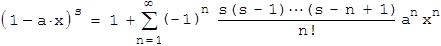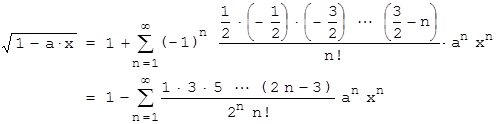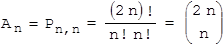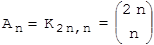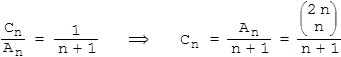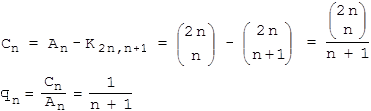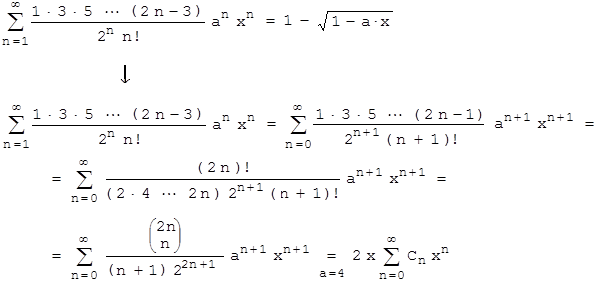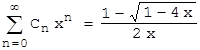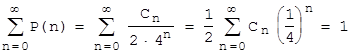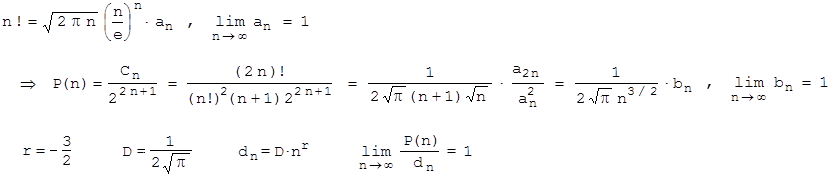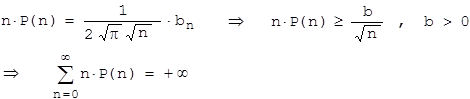Vom Theaterkassenproblem über die Catalan-Zahlen zur Familienplanung
Die Lösung steht im unteren Teil der Seite.
Wir stellen ein (natürlich hypothetisches) Problem der Familienplanung vor: In einem Land strebt jede Mutter an, solange Kinder zu bekommen, bis sie genau einen Jungen mehr hat als Mädchen. Es soll uns hier nicht kümmern, dass das kaum praktikabel erscheint. Aber aus dieser Strategie entstehen eine Reihe von Fragen, u.a. diese: Wie groß ist die Wahrscheinlichkeit, dass es einer Mutter nie gelingt, ihr Ziel zu erreichen, selbst wenn sie beliebig viele Kinder bekommen könnte? Wieviele Kinder hat eine Mutter im Durchschnitt? Wird es in diesem Land auf Dauer mehr Jungen als Mädchen geben?
Um zur Lösung zu gelangen, machen wir einen Umweg und fangen bei einem gut bekannten anderen Problem an, dem Theaterkassenproblem.
| |
Theaterkassenproblem
Eine Eintrittskarte für eine Theatervorstellung kostet 50 Euro. Es hat sich an der Kasse eine Schlange von 2n Besuchern gebildet, von denen n einen 50-Euro-Schein haben und die anderen n einen 100-Euro-Schein. Bei Beginn des Kartenverkaufs hat der Kassierer kein Wechselgeld. Mit welcher Wahrscheinlichkeit qn erlaubt die (zufällige) Reihenfolge der Besucher in der Schlange eine lückenlose Abfertigung an der Kasse? (Der Kassierer soll also jedem Besucher, der einen 100-Euro-Schein hinlegt, sofort einen bereits eingenommenen 50-Euro-Schein zurückgeben können.) |
|
Die Lösung des Theaterkassenproblems kann leicht durch Probieren gefunden werden. Zunächst soll eine Notation vereinbart werden, die die Warteschlange beschreibt. Ein "+" soll für einen 50-Euro-Schein und ein "-" für einen 100-Euro-Schein stehen. Für n = 6 würde diese Warteschlange problemlos abgefertigt:
+ - + + - + - - + + - -
Die folgende Warteschlange könnte nicht der Reihe nach bedient werden:
+ + + - - - - + + - + -
Wir betrachten also endliche Folgen aus "+" und "-" der Länge 2n mit gleich vielen "+" und "-" . Solche Folgen wollen wir n-ausgeglichen nennen. Aus kombinatorischer Sicht handelt es sich um Permutationen mit Wiederholung. Bei der ersten Warteschlange ist nach jedem Abschnitt der Folge die Anzahl der "+" mindestens so groß wie die Anzahl der "-" . Solche Folgen sollen +führend genannt werden. Die zweite Folge ist nicht +führend.
Aufgabe 1
Berechnen Sie die Anzahl An der n-ausgeglichenen Folgen.
Aufgabe 2
Bestimmen Sie die Anzahl Cn der +führenden Folgen unter den n-ausgeglichenen Folgen für n ≤ 4 .
Aus Cn/An ergibt sich eine Vermutung für eine allgemeine Formel der Cn .
Das geht ziemlich schnell durch Ausprobieren, wenn man beachtet, dass vorne immer ein "+" und hinten immer ein "-" stehen muss. Für n = 4 bleiben dann nur noch 6 freie Plätze, die für die +führenden Folgen gefüllt werden müssen.
Die Cn bilden die Folge der Catalan-Zahlen, die eine wichtige Rolle in der diskreten Mathematik spielen. Die Vermutung aus Aufgabe 2 wird in vielen Quellen mit Hilfe einer erzeugenden Funktion bewiesen, aber es gibt auch einen eleganten elementaren Beweis. Dazu stellen wir die Folge der n-ausgeglichenen Folgen graphisch dar. Wir zeichnen einen Pfad in 2n Schritten von (0,0) nach (2n,0) ; einem "+" entspricht eine Diagonale von (a,b) nach (a+1,b+1) und einem "-" eine Diagonale von (a,b) nach (a+1,b-1) . Die beiden Folgen unterhalb des Theaterkassenproblems hätten dann die folgenden Darstellungen:
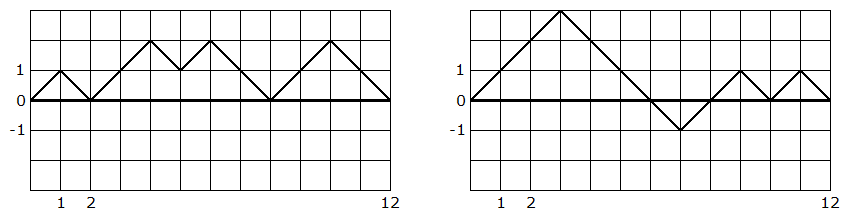
Die +führenden Folgen werden durch Pfade dargestellt, die nirgends durch die untere Halbebene verlaufen.
Um die Formel für die Catalan-Zahlen zu beweisen, berechnet man zuerst die Anzahl der Folgen, die nicht +führend sind, und subtrahiert dann diese Anzahl von An . Dazu ein Tipp: Die nicht +führenden Folgen der Länge 2n haben die gleiche Anzahl wie alle Folgen der Länge 2n mit n-1 "+" und n+1 "-" . Um sich dies zu veranschaulichen, ist die graphische Darstellung hilfreich.
Aufgabe 3
Bestimmen Sie Cn für alle n ∈ N (mit Beweis).
Lösen Sie damit das Theaterkassenproblem.
Bevor wir endlich zum eigentlichen Problem der Familienplanung kommen, soll noch eine Anwendung der Catalan-Zahlen in der Graphentheorie erwähnt werden, die planaren Bäume. Hier ist ein Bild eines planaren Baums:
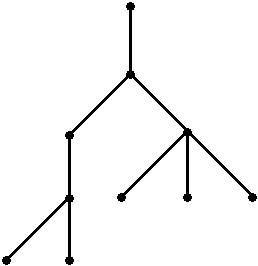
Das Bild zeigt einen hierarchischen (in Ebenen angeordneten) Graphen, der auf der obersten Ebene nur einen Knoten hat (die Wurzel). Alle Knoten können zur darunter liegenden Ebene endlich viele Verzweigungen haben, aber alle Knoten außer der Wurzel haben genau eine Kante zur nächsthöheren Ebene. Es gibt keine Kanten innerhalb einer Ebene. Für die Bestimmung der Anzahl planarer Bäume ist die Orientierung links-rechts von Bedeutung, d.h. in dem abgebildeten Baum würde durch die Vertauschung der beiden Knoten auf der dritten Ebene (mitsamt ihren Unterbäumen) ein anderer planarer Baum entstehen. Hat ein solcher Baum n+1 Knoten, so lässt er sich durch eine +führende n-ausgeglichene Folge beschreiben. (Tipp: Man durchlaufe den Baum von der Wurzel durch alle Knoten bis zurück zur Wurzel und unterscheide n Abwärtsschritte und n Aufwärtsschritte.)
Aufgabe 4
Zeigen Sie: Es gibt Cn planare Bäume mit n+1 Knoten.
Ausgehend von der Anwendung der Catalan-Zahlen bei planaren Bäumen wird nun zusätzlich C0 = 1 definiert. Dies harmoniert auch mit der in Aufgabe 3 hergeleiteten Formel.
Nun zur Familienplanung, wie sie zu Beginn beschrieben wurde. Offenbar haben alle Mütter, die das Ziel erreicht haben, eine ungerade Anzahl 2n+1 von Kindern, also n+1 Jungen und n Mädchen, n ∈ N0. Die Folge der Kinder notieren wir mit "+" für die Mädchen und mit "-" für die Jungen. Hier sind die beiden möglichen Kinderfolgen bei 5 Kindern (n = 2) :
+ + - - -
+ - + - -
Der Zusammenhang mit dem Theaterkassenproblem und den Catalan-Zahlen ist leicht erkennbar. Wir wollen unterstellen, dass Mädchen und Jungen jeweils mit Wahrscheinlichkeit 1/2 geboren werden.
Aufgabe 5
Wie groß ist die Wahrscheinlichkeit pn , dass eine Mutter genau 2n+1 Kinder bekommt?
Es soll nun gezeigt werden, dass P(n)= pn eine diskrete Wahrscheinlichkeitsverteilung auf N0 ist, d.h. Σn≥0 P(n) = 1 . Das hat eine wichtige Konsequenz: Das Ereignis "1 Junge mehr" stellt sich irgendwann sicher ein. Anders ausgedrückt: Die Wahrscheinlichkeit, dass eine Mutter trotz beliebig vieler Versuche auf Dauer mindestens so viele Mädchen wie Jungen unter ihren Kindern hat, ist 0 .
Die Lösung von Aufgabe 5 zeigt uns, dass es für die Berechnung von Σn≥0 P(n) ausreicht, wenn wir Σn≥0 Cn·xn als geschlossene Funktion f(x) ausdrücken können. Die Summe ist dann die Potenzreihe zu f(x) und heißt erzeugende Funktion der Cn . Dies ist der schwierigste Teil auf dieser Problemseite, aber es wird Schritt für Schritt durch den Beweis geführt.
f(x) hat also eine Potenzreihe, deren Koeffizienten Cn bekannt sind. Für sehr viele Funktionen finden sich die zugehörigen Potenzreihen in Tafelwerken oder im Internet. In der Hoffnung, dass man unter den gängigen Reihen fündig wird, stößt man schnell auf die Binomialreihe:
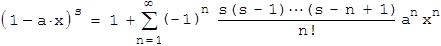
a kann später noch passend gewählt werden. Für s muss man ein wenig probieren, damit die Reihe zu den Catalan-Zahlen passt. s = 1/2 erweist sich als guter Kandidat:
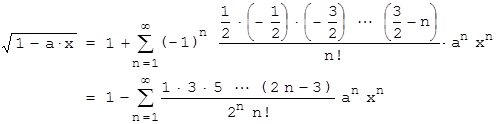
Die letzte Reihe führt mit Indexverschiebung und geeigneter Wahl von a auf die gesuchte Potenzreihe, d.h. auf die erzeugende Funktion der Cn . Behalten Sie dabei auch den Konvergenzbereich der Potenzreihe im Auge.
Aufgabe 6
Beweisen Sie Σn≥0 P(n) = 1 mit Hilfe der erzeugenden Funktion für Cn .
Aufgabe 7
Die P(n) verhalten sich für n > 0 näherungsweise wie d n = D· nr . Bestimmen Sie r und D mit Hilfe der Stirling'schen Formel.
Aufgabe 8
Wird es in diesem Land auf Dauer mehr Jungen als Mädchen geben?
Aufgabe 9
Welcher Anteil der Mütter ist spätestens nach dem 5., 11. bzw. 21. Kind am Ziel angelangt?
Aufgabe 10
Berechnen Sie den Erwartungswert für die Anzahl der Kinder pro Mutter.
Auch hier hilft die Stirling'sche Formel.
Lösung
Aufgabe 1
Berechnen Sie die Anzahl An der n-ausgeglichenen Folgen.
Kombinatorischer Ansatz:
Permutationen mit Wiederholung (Reihenfolgen von 2n Elementen mit je n gleichen Elementen):
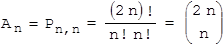
Oder: Kombinationen ohne Wiederholung (Auswahl von n Plätzen für "+" aus 2n möglichen Plätzen):
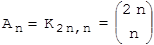
Aufgabe 2
Bestimmen Sie die Anzahl Cn der +führenden Folgen unter den n-ausgeglichenen Folgen für n ≤ 4 .
Aus Cn/An ergibt sich eine Vermutung für eine allgemeine Formel der Cn .
n = 1 + - C1 = 1 A1 = 2 C1/A1 = 1/2
n = 2 + + - -
+ - + - C2 = 2 A2 = 6 C2/A2 = 1/3
n = 3 + + + - - -
+ + - + - -
+ + - - + -
+ - + + - -
+ - + - + - C3 = 5 A3 = 20 C3/A3 = 1/4
n = 4 + + + + - - - -
+ + + - + - - -
+ + + - - + - -
+ + + - - - + -
+ + - + + - - -
+ + - + - + - -
+ + - + - - + -
+ + - - + + - -
+ + - - + - + -
+ - + + + - - -
+ - + + - + - -
+ - + + - - + -
+ - + - + + - -
+ - + - + - + - C4 = 14 A4 = 70 C4/A4 = 1/5
Vermutung:
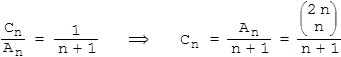
Aufgabe 3
Bestimmen Sie Cn für alle n ∈ N .
Lösen Sie damit das Theaterkassenproblem.
Wie folgen dem Tipp: Es gibt genau so viele Folgen aus n-1 "+" und n+1 "-" wie nicht +führende n-ausgeglichene Folgen.
Aus einer nicht +führenden n-ausgeglichenen Folge kann man eine eine Folge herstellen, in der zwei "-" mehr als "+" vorhanden sind, indem man unmittelbar nach der ersten Stelle, an der erstmals die "-" die "+" überholen, alle "+" in "-" umwandelt und umgekehrt. Dadurch entsteht in der graphischen Darstellung ein Pfad, der bei (2n,-2) endet. Das soll am zweiten Beispiel aus der Aufgabenstellung gezeigt werden:
+ + + - - - - + + - + - → + + + - - - -|- - + - +
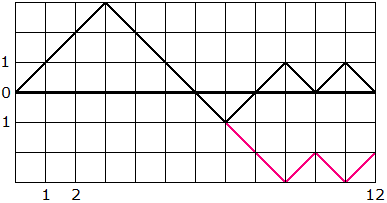
Dadurch entsteht eine bijektive Abbildung zwischen den beiden Mengen von Folgen, denn es gibt eine Umkehrabbildung: In einer Folge aus n-1 "+" und n+1 "-" (die also in (2n,-2) endet) werden unmittelbar nach der ersten Stelle, an der erstmals die "-" die "+" überholen, alle "+" in "-" umgewandelt und umgekehrt. Dadurch entsteht eine nicht +führende n-ausgeglichene Folge. Dazu ein Beispiel:
- - + + + - - + - - + - → -|+ - - - + + - + + - +
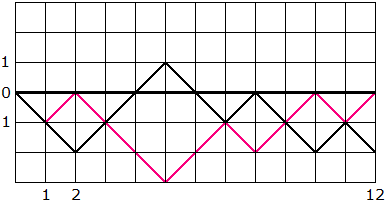
Die Anzahl der Folgen mit n-1 "+" und n+1 "-" berechnet man wieder über Kombinationen wie in Aufgabe 1 und erhält K2n,n+1 . Daraus folgt für die Catalan-Zahlen Cn und die gesuchte Wahrscheinlichkeit qn aus dem Theaterkassenproblem:
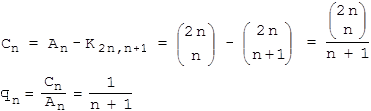
Aufgabe 4
Zeigen Sie: Es gibt Cn planare Bäume mit n+1 Knoten.
Es wird ein Weg durch einen planaren Baum mit n+1 Knoten beschrieben:
- Man beginnt an der Wurzel und umrundet den Baum an der "Außenseite", links beginnend (man kann sich dafür die Kanten als Straßen mit zwei Rändern vorstellen).
- Läuft man eine Kante abwärts, so notiert man dort ein "+" , läuft man eine Kante aufwärts, so notiert man dort ein "-".
- So wird jede Kante zweimal durchlaufen, und es werden gleich viele "+" und "-" notiert.
- Da es an jeder Kante erst abwärts und später aufwärts geht, erhält man eine +führende Folge.
- Da jede Kante genau einen unteren Knoten hat, und umgekehrt jeder Knoten (außer der Wurzel) genau eine Kante nach oben hat, hat der Graph n Kanten. Die vollständige Folge ist also n-ausgeglichen.
Der Durchlauf durch einen planaren Baum wird durch das folgende Beispiel illustriert. Die Nummern stehen für die Reihenfolge der Schritte.
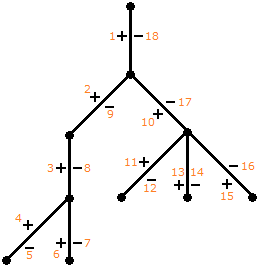
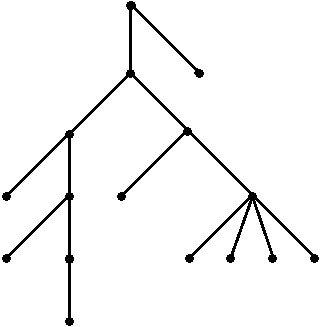
Liegt nun umgekehrt eine n-ausgeglichene +führende Folge vor, so lässt sich daraus in eindeutiger Weise ein planarer Baum mit n+1 Knoten erstellen. Dazu sehe man sich das folgende Beispiel für n = 15 an:
| + + + - + + - + + - - - - + + - + + - + - + - + - - - - + - |
 |
|
Es gibt also genau so viele planare Bäume mit n+1 Knoten wie n-ausgeglichene +führende Folgen.
Aufgabe 5
Wie groß ist die Wahrscheinlichkeit pn , dass eine Mutter genau 2n+1 Kinder bekommt?
Unter den ersten 2n Kindern müssen gleich viele Mädchen und Jungen sein, und die Jungen dürfen nie in der Überzahl gewesen sein. Das (2n+1)-te Kind muss ein Junge sein. Also gibt es Cn Geschwisterfolgen, die nach dem (2n+1)-ten Kind abbrechen, unter den insgesamt 22n+1 möglichen Geschwisterfolgen bis zum (2n+1)-ten Kind.
pn = Cn/22n+1
Aufgabe 6
Beweisen Sie Σn≥0 P(n) = 1 mit Hilfe der erzeugenden Funktion für Cn .
Wir hatten P(n)= pn gesetzt; pn wurde in Aufgabe 5 berechnet und enthält Cn . In der Aufgabenstellung sind wir auf eine Reihe gestoßen, die eine Ähnlichkeit zur erzeugenden Funktion der Cn aufweist. Da diese aber bei n = 0 beginnt, machen wir eine Indexverschiebung und erhalten nach kleineren Umformungen das gewünschte Ergebnis:
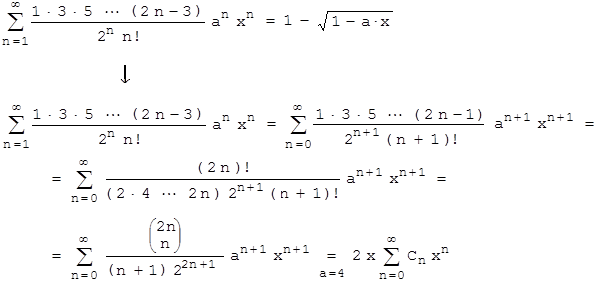
Vergleicht man in dieser Rechnung die erste und die letzte Zeile, so ergibt sich:
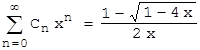
Für den Konvergenzbereich dieser Binomialreihe gilt ax ∈ [-1,1] , also x ∈ [-1/4, 1/4] .
Zur Lösung der Aufgabe muss jetzt nur noch x = 1/4 in die erzeugende Funktion der Cn eingesetzt werden:
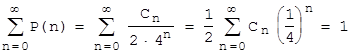
Aufgabe 7
Die P(n) verhalten sich für n > 0 näherungsweise wie d n = D· nr . Bestimmen Sie r und D mit Hilfe der Stirling'schen Formel.
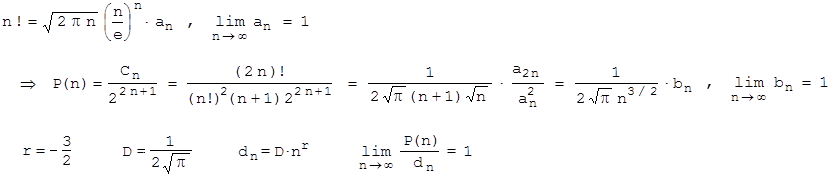
Aufgabe 8
Wird es in diesem Land auf Dauer mehr Jungen als Mädchen geben?
Natürlich nicht. Die Wahrscheinlichkeit für Mädchen/Jungen bleibt je 1/2 und lässt sich durch keine Strategie aushebeln. Es wird in diesem Land zu jedem Zeitpunkt viele Mütter geben, die genau einen Jungen mehr haben als Mädchen, aber viele andere Mütter sind noch nicht "fertig" und haben mehr Mädchen.
Aufgabe 9
Welcher Anteil der Mütter ist spätestens nach dem 5., 11. bzw. 21. Kind am Ziel angelangt?
5. Kind n = 2 Σn≤2 P(n) = 0,6875
11. Kind n = 5 Σn≤5 P(n) ≈ 0,7744
21. Kind n = 10 Σn≤10 P(n) ≈ 0,8318
Man erkennt, wie langsam die aufsummierten Wahrscheinlichkeiten wachsen. Diese Familienstrategie ist u.a. deshalb kaum praktikabel.
Aufgabe 10
Berechnen Sie den Erwartungswert für die Anzahl der Kinder pro Mutter. (Gemeint sind die Mütter, die bereits n+1 Jungen und n Mädchen haben.)
Wir berechnen statt dessen der Einfachheit halber den Erwartungswert für die Anzahl n der Mädchen. Aus Aufgabe 7 folgt für n > 0 :
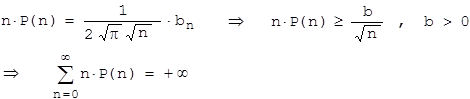
Die Verteilung für die Kinderzahl hat keinen endlichen Erwartungswert! Das passt tendenziell zu den Zahlen in Aufgabe 9. Die Familienstrategie hat einen Trend zu sehr großen Kinderzahlen pro Mutter, da es sehr lange dauern kann, bis das Ziel erreicht ist.
Publiziert 2014-10-14 Stand 2014-01-19
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite