Der Rhesus-Faktor
Die Lösung steht im unteren Teil der Seite.
Bei der Angabe der Blutgruppe eines Menschen findet man häufig am Ende ein "+" oder "-". Dieses steht für den Rhesusfaktor; z.B. liest sich "A+" als "Blutgruppe A, Rhesus-positiv" oder "0-" als "Blutgruppe 0, Rhesus-negativ". Der Rhesusfaktor ist ein Kennzeichen der roten Blutkörperchen. Dieses genetische Merkmal wird nach einfachen Regeln der Mendel'schen Vererbungslehre an die Nachkommen weitergegeben.
Entscheidend für die Ausprägung des Rhesusfaktors ist ein bestimmtes Chromosomenpaar als Träger der entsprechenden Information. Auf jedem der beiden Chromosomen in diesem Paar ist entweder die Erbanlage für "Rhesus-positiv" vorhanden (bezeichnet mit D ) oder sie fehlt ("Rhesus-negativ", bezeichnet mit d ). Somit können drei Kombinationen ("Rhesus-Typen") vorkommen: DD, Dd, dd.
Die Erbanlage D ist dominant, d.h. sowohl DD als auch Dd machen das Blut des Trägers Rhesus-positiv; rein äußerlich lassen sich also DD und Dd nicht unterscheiden. Nur Menschen mit der genetischen Information dd haben somit Rhesus-negatives Blut.
Die Vererbung des Rhesus-Faktors von den Eltern auf ein Kind folgt den Mendel'schen Regeln. Sowohl von der Mutter als auch vom Vater geht von dem Chromosomenpaar, das die Rhesus-Information trägt, jeweils ein Chromosom auf das Kind über - die Auswahl ist zufällig -, und so entsteht beim Kind wieder ein Paar. Haben also Mutter und Vater beispielsweise beide den Rhesus-Typ DD , so auch das Kind. Haben die Eltern die Konstellation DD-dd , so hat das Kind Dd . Liegt bei den Eltern DD-Dd vor, so kann das Kind DD oder Dd aufweisen; bei Dd-Dd können beim Kind alle drei Rhesus-Typen auftreten, usw.
Rhesus-negative Menschen kommen fast ausschließlich in Europa und in den von Europäern kolonialisierten Ländern wie z.B. Nordamerika vor. Die Auftretenshäufigkeit schwankt weltweit stark, ist aber regional recht stabil. In Deutschland und in Westeuropa sind etwa 15 % der Menschen Rhesus-negativ. Warum ist der Rhesus-Faktor so wichtig, dass er bei der Blutgruppe angegeben wird? Im "normalen" Leben spielt er keine Rolle. Aber er ist von großer Bedeutung bei der Verwendung von Blutkonserven. Rhesus-negative Menschen dürfen kein Rhesus-positives Blut erhalten, da sie dagegen Antikörper bilden; darauf muss also bei der Gabe von Blutkonserven streng geachtet werden. Während sich dies relativ leicht organisieren lässt, gibt es aber eine andere Gefahrenquelle, die nur durch ärztlichen Eingriff beherrscht werden kann. Gemeint ist die erste Schwangerschaft einer Rhesus-negativen Frau mit einem Rhesus-positiven Baby. Zwischen Mutter und Kind kann es leicht zu einer geringfügigen Vermengung des Blutes kommen, vor allem während der Geburt. Falls das (in seltenen Fällen) schon vor der Geburt geschieht, kann das Kind durch den Kontakt mit den mütterlichen Antikörpern geschädigt werden; spätestens aber bei der zweiten Schwangerschaft mit einem Rhesus-positiven Kind ist das Baby durch den Kontakt mit den mütterlichen Antikörpern extrem gefährdet. Deshalb erhalten solche Mütter heutzutage rechtzeitig ein Gegenmittel, das die Ausbildung der Antikörper verhindert. Knapp 10 % aller Schwangerschaften in Deutschland weisen diese kritische Konstellation auf: Mutter dd , Kind Dd .
Wie kommt hier die Mathematik ins Spiel? Man muss ein wenig rechnen und an einer Stelle eine kubische Gleichung lösen, um alle Zusammenhänge rund um den Rhesus-Faktor aufzuklären. Die folgenden Fragen sollen beispielhaft zeigen, um was es u.a. geht:
- Lässt sich aus dem Anteil Rhesus-negativer Menschen in der Bevölkerung der Anteil der Rhesus-unverträglichen Schwangerschaften bestimmen? (Antwort: ja)
- Umgekehrt: Lässt sich aus dem Anteil der Rhesus-unverträglichen Schwangerschaften der Anteil Rhesus-negativer Menschen in der Bevölkerung bestimmen? (Antwort: nein)
- Bleibt der Anteil der Rhesus-negativen Menschen stabil? (Antwort: ja, fast)
- Wieviele Rhesus-unverträgliche Schwangerschaften können maximal auftreten (in %) ?
Nun wollen wir den Rhesus-Faktor und seine Vererbungsregeln systematisch untersuchen.
Aufgabe 1
Vervollständigen Sie die folgende Tabelle. In den leeren Feldern sollen die Wahrscheinlichkeiten für DD, Dd, dd beim Kind eingetragen werden.
| Mutter ↓ Vater → |
DD |
Dd |
dd |
| DD |
|
DD 0.5 Dd 0.5 |
|
| Dd |
|
|
|
| dd |
|
|
dd 1.0 |
Für alles Weitere ist die Festlegung einiger Bezeichnungen wichtig. Die folgenden p(·) stehen für Auftretens-Wahrscheinlichkeiten in einer bestimmten Population:
p(D)
p(d)
p(+)
p(-)
p(DD)
p(Dd)
p(dd)
p(u)
Die beiden ersten Wahrscheinlichkeiten beziehen sich auf ein einzelnes, zufällig ausgewähltes Rhesus-Chromosom. "+" und "-" beziehen sich auf die Erbanlagen "Rhesus-positiv" bzw. "Rhesus-negativ" bei zufällig ausgewählten Menschen. "u" steht für die Rhesus-Unverträglichkeit bei einer Schwangerschaft.
Aufgabe 2
Jeder Mensch hat zwei Chromosomen, die D oder d tragen. Wir betrachten nun alle diese (einzelnen) Chromosomen in einer (großen) Population. Wie ermittelt man den Anteil der d-Chromosomen, also p(d), in diesem Pool? Die Chromosomen selbst lassen sich nur schwer untersuchen, aber die Verteilung der Blutgruppen und damit des Rhesusfaktors ist bekannt, also p(+) und p(-) (siehe oben für Deutschland). Es gibt noch einen zweiten Hinweis: Die Häufigkeit der "kritischen Schwangerschaften" p(u). Die oben genannten Zahlen p(-) und p(u) für Deutschland sind nur ungefähre Werte. Lassen sie sich miteinander vereinbaren?
Aufgabe 3
Jetzt kommt die interessante und naheliegende Frage: Verändert sich der Anteil der Rhesus-negativen Menschen in einer Population im Lauf der Zeit?
Wir beginnen mit einem Gedankenexperiment. Wir stellen eine Population ("0. Generation") aus Männern und Frauen willkürlich zusammen, mit der folgenden Verteilung der Chromosomen-Paare:
aw = p(DD|weibl)
bw = p(Dd|weibl)
cw = p(dd|weibl)
am = p(DD|männl)
bm = p(Dd|männl)
cm = p(dd|männl)
Jede Dreiergruppe ergibt in der Summe 1 . Mit der Tabelle aus Aufgabe 1 kann man nun die Anteile p(DD), p(Dd), p(dd) für die Folgegenerationen berechnen; diese Anteile hängen naturgemäß nicht mehr vom Geschlecht ab.
Aufgabe 3, Teil 1
Rechnen Sie zunächst ein konkretes Beispiel für die Anteile an = p(DD), bn = p(Dd), cn = p(dd) in der n-ten Generation (d.h. n-ten Nachkommengeneration) für n = 1, 2, 3 ... mit beliebigen Startwerten 0 < aw < 1 usw. Was stellen Sie fest?
Ab der 2. Generation lässt sich die Rechnung in eine einfache Formel fassen:
(an+1, bn+1, cn+1) = f(an, bn, cn) n = 1, 2, 3 ...
Bestimmen Sie die Funktion f .
Aufgabe 3, Teil 2
Wie verändert sich der Anteil der d-Chromosomen im Chromosomen-Pool?
Aufgabe 3, Teil 3
Was folgt aus Teil 2 für die Stabilität von (an, bn, cn) ? Rechnen Sie das auch mit Hilfe der Funktion f nach, indem Sie (an, bn, cn) durch p(d) ausdrücken.
Geben Sie eine zusammenfassende Antwort auf den dritten Spiegelpunkt vor Aufgabe 1.
Aufgabe 4
Jetzt wollen wir nur "Rhesus-stabile" Populationen betrachten. Das bedeutet, dass p(d) ∈ (0,1) bekannt ist und sich daraus die Anteile p(DD), p(Dd), p(dd) bestimmen lassen.
Vor der Aufgabe 2 stehen acht Wahrscheinlichkeiten. Sechs von ihnen sind "äquivalent" in dem Sinne, dass sie sich gegenseitig eindeutig ineinander umrechnen lassen. Dies gilt nicht für p(Dd) und p(u). Die Äquivalenz der sechs Wahrscheinlichkeiten ist leicht zu zeigen. Warum gilt sie nicht für die beiden letztgenannten?
Was folgt für die anderen Wahrscheinlichkeiten, wenn p(Dd) bzw. p(u) bekannt ist?
Ein Nebenresultat ist: Der Anteil der Menschen mit "gemischten" Rhesus-Chromosomen beträgt maximal 50 % , d.h. es gilt p(Dd) ≤ 0.5 .
Bestimmen Sie auch den maximal möglichen Anteil Rhesus-unverträglicher Schwangerschaften (siehe letzter Spiegelpunkt vor Aufgabe 1).
Nun lassen sich auch die beiden ersten Spiegelpunkte vor Aufgabe 1 präzise beantworten. Was ergibt sich für das Beispiel p(u) = 0.09 ?
Lösung
Aufgabe 1
| Mutter ↓ Vater → |
DD |
Dd |
dd |
| DD |
DD 1.0 |
DD 0.5 Dd 0.5 |
Dd 1.0 |
| Dd |
DD 0.5 Dd 0.5 |
DD 0.25 Dd 0.5 dd 0.25 |
Dd 0.5 dd 0.5 |
| dd |
Dd 1.0 |
Dd 0.5 dd 0.5 |
dd 1.0 |
Aufgabe 2
p(d) lässt sich aus dem Anteil der Rhesus-negativen Menschen berechnen:
p(-) = p(dd) = p(d)2 → p(d) = p(-)1/2
Nun liegt es nahe, auch p(u) durch p(d) auszudrücken. Die Wahrscheinlichkeit für eine Rhesus-negative Mutter ist p(dd) = p(d)2. Das Kind soll Rhesus-positiv (Typ Dd ) sein, hat also vom Vater ein D ; die Wahrscheinlichkeit dafür beträgt p(D) = 1 - p(d). Also gilt:
p(u) = p(d)2·(1 - p(d))
Mit p(-) = 0.15 erhalten wir näherungsweise p(d) = 0.3873 und damit p(u) = 0,0919. Die eingangs angegebenen Prozentwerte von ca. 15 % und knapp 10 % sind also plausibel.
Aufgabe 3
Die Erbanlage D ist dominant. Man könnte daraus den Schluss ziehen, dass die Erbanlage d mit der Zeit verschwindet. Wir werden sehen, dass das falsch ist.
Teil 1
Zu unserem Gedankenexperiment: Wir gehen davon aus, dass sich die Population durch zufällige Paarungen fortpflanzt, und berechnen mit der Tabelle aus Aufgabe 1 die Anteile a1 = p(DD), b1 = p(Dd), c1 = p(dd) in der 1. Generation:
a1 = aw·am + aw·bm /2 + bw·am /2 + bw·bm /4
b1 = aw·bm /2 + aw·cm + bw·am /2 + bw·bm /2 + bw·cm /2 + cw·am + cw·bm /2
c1 = bw·bm /4 + bw·cm /4 + cw·bm /2 + cw·cm
a1, b1, c1 sind bei Frauen und Männern gleich. Mit Hilfe der Tabelle aus Aufgabe 1 erhält man für die weiteren Generationen:
(an+1, bn+1, cn+1) = f(an, bn, cn) = (an2 + an·bn + bn2/4, an·bn + 2·an·cn + bn2/2 + bn·cn , bn2/4 + bn·cn + cn2)
Beispielrechnung:
aw = 0.6
bw = 0.3
cw = 0.1 a1 = 0.45 a2 = 0.455625 a3 = 0.455625
b1 = 0.45 b2 = 0.43875 b3 = 0.43875
am = 0.4 c1 = 0.1 c2 = 0.105625 c3 = 0.105625
bm = 0.4
cm = 0.2
Man stellt fest, dass die Werte (an, bn, cn) ab der 2. Generation konstant bleiben.
Teil 2
Teil 1 legt die Annahme nahe, dass in einer geschlossenen Population - die sich also nur untereinander fortpflanzt - auch p(d) über die Generationen konstant bleibt, denn p(d)2 = cn . Diese Stabilität des Anteils p(d) in der Bevölkerung gilt in unserem Gedankenexperiment ab der 1. Generation, also sobald die Anteile für DD , Dd und dd bei Frauen und Männern gleich sind. Das kann man sich leicht klar machen: Ein beliebig herausgegriffenes Rhesus-Chromosom kommt entweder von der Mutter oder vom Vater, und bei beiden ist die Wahrscheinlichkeit für die Erbanlage d gleich p(d).
Teil 3
Es gilt für n ≥ 2 :
cn = p(d)2
an = (1 - p(d))2
bn = 1 - an - cn
Die Stabilität von (an, bn, cn) über die Generationen, die in Teil 1 nur beispielhaft gezeigt wurde, folgt also aus der Stabilität von p(d).
Für jedes vorgegebene p(d) ist folglich (an, bn, cn) ein Fixpunkt von f , d.h. (an, bn, cn) = f(an, bn, cn). Das wollen wir auch durch Rechnung nachweisen. Nach der Tabelle in Aufgabe 1 gilt allgemein (die Indizes werden der Übersichtlichkeit halber fortgelassen):
f(a, b, c) = (a2 + ab + b2/4, ab + 2ac + b2/2 + bc, b2/4 + bc + c2)
Setzt man nun wie oben c = p(d)2, a = (1 - p(d))2, b = 1 - a - c , so ergibt sich nach ein wenig Rechenarbeit f(a, b, c) = (a, b, c) .
f lässt sich noch einfacher ausdrücken, wenn man c = 1 - a - b beachtet und zur Abkürzung w = a + b/2 setzt:
f(a, b, c) = (w2, 2w(1-w), (1-w)2)
Zusammenfassend stellen wir fest, dass in einer geschlossenen Population alle Rhesus-Werte wie z.B. p(-) und p(u) konstant bleiben. Selbst wenn man willkürlich eine Population zusammenstellt, wird sich diese Stabilität spätestens ab der Enkelgeneration einstellen.
Aufgabe 4
Sechs Wahrscheinlichkeiten lassen sich eindeutig ineinander umrechnen:
1 - p(+) = p(-) = p(dd) = p(d)2 = (1 - p(D))2
p(DD) = p(D)2
Anders sieht es bei p(Dd) aus. Wir führen diese Größe auf p(d) zurück:
p(Dd) = 1 - p(DD) - p(dd) = 1 - (1 - p(d))2 - p(d)2 = 2·p(d)·(1 - p(d))
Also lässt sich p(Dd) eindeutig aus p(d) (und aus den anderen äquivalenten Wahrscheinlichkeiten) bestimmen, aber die Umkehrung gilt nicht. Man erhält aus p(Dd) die Lösungen einer quadratischen Gleichung für p(d) :
p(d) = ( 1 - ( 1 - 2·p(Dd))1/2 ) / 2
p(d) = ( 1 + ( 1 - 2·p(Dd))1/2 ) / 2
Aus p(Dd) = 2·p(d)·(1 - p(d)) folgt p(Dd) ≤ 0.5 (rechte Seite nach p(d) ableiten). Beide Lösungen der quadratischen Gleichung liegen symmetrisch zu 0.5 im Intervall (0,1) .
Eine eindeutige Lösung gibt es nur für p(Dd) = 0.5 ; dann ist auch p(d) = 0.5 .
Noch interessanter ist die Beziehung zwischen p(u) und p(d), die wir aus Aufgabe 2 kennen:
p(u) = p(d)2·(1 - p(d))
Während sich p(u) eindeutig aus p(d) berechnen lässt (das haben wir in Aufgabe 2 durchgeführt), ist mit einem vorgegebenen p(u) eine kubische Gleichung für p(d) zu lösen.
Diese Gleichung wollen wir uns näher anschauen. Wir setzen x = p(d) und g(x) = x2 - x3 . g hat Nullstellen in 0 und 1 und ein Maximum in x = 2/3 mit g(2/3) = 4/27 = 0.148148... Also können in jeder Population maximal ca. 14.8 % der Schwangerschaften Rhesus-unverträglich sein.
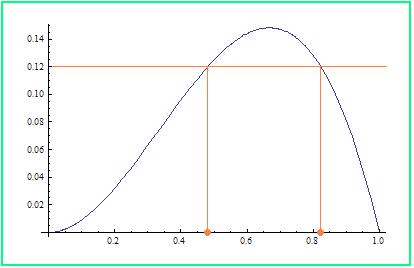
Die Grafik zeigt den Graphen von g . Jeder der möglichen Werte von p(u) hat zwei korrespondierende Werte für p(d), mit Ausnahme des Maximums p(u) = 4/27 ; in der Grafik ist das für p(u) = 0.12 dargestellt.
Es bleibt noch die Frage, ob p(Dd) und p(u) in eindeutiger Weise zusammenhängen. Dies ist nicht der Fall. Dazu schauen wir uns die folgenden Gleichungen an:
p(u) = p(Dd)·(p(d)/2)
p(Dd) = p(u)·(2/p(d))
Ist also p(Dd) gegeben, so ergeben sich zwei verschiedene Werte für p(u), da p(d) zwei verschiedene Werte annehmen kann (außer bei p(Dd) = 0.5 ).
Ist umgekehrt p(u) gegeben, so ergeben sich zwei verschiedene Werte für p(Dd) (außer bei p(u) = 4/27 ).
Nun kann man die beiden ersten Spiegelpunkte vor Aufgabe 1 beantworten:
Der Anteil Rhesus-negativer Menschen ist p(-) = p(d)2. Wegen p(u) = p(d)2·(1 - p(d)) erhält man:
p(u) = p(-)·(1 - p(-)1/2)
Ist p(u) bekannt, so gehören dazu zwei Werte für p(d), also auch zwei Werte für p(-). Ist beispielsweise p(u) = 0.09 , so ergibt die Lösung der kubischen Gleichung näherungsweise p(d) = 0.3814 und p(d) = 0.8851 ; es folgen die Lösungen p(-) = 0.1455 und p(-) = 0.7834 .
Publiziert 2010-09-26 Stand 2010-07-31
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite
