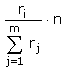
Kamele. Da der Pilger seine k Kamele zurückerhalten soll, muss außerdem gelten:
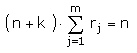
Daraus folgt aber
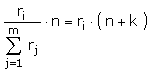
Also ist die Erbaufteilung gerecht.
| Manfred Börgens Mathematische Probleme # 24 |
Liste aller Probleme mit Lösungen voriges Problem nächstes Problem |
zur Leitseite |
Die folgende kleine mathematische Erzählung ist sehr bekannt und sehr alt.
Es lebte in Arabien ein alter Vater, der drei Söhne und 17 Kamele hatte. Als der Greis sein Ende nahen fühlte, versammelte er die Söhne um sich und sprach zu ihnen: "Alles was ich euch hinterlasse, sind meine Kamele. Teilt sie so, dass der Älteste die Hälfte, der Mittlere ein Drittel und der Jüngste ein Neuntel erhält." Kaum war dies verkündet, da schloss er die Augen, und die Söhne konnten ihn nicht mehr darauf aufmerksam machen, dass sein letzter Wille offenbar unvollstreckbar sei. Siebzehn ist doch eine störrische Zahl und lässt sich weder durch zwei noch durch drei und schon gar nicht durch neun teilen! Doch der letzte Wille des Vaters ist jedem braven Araber heilig. Da kam zum Glück ein weiser Pilger auf seinem Kamel daher geritten, der sah die Ratlosigkeit der drei Erben und bot ihnen seine Hilfe an. Sie trugen ihm den verzwickten Fall vor, und der Weise riet lächelnd, sein eigenes Kamel zu den hinterlassenen zu stellen und die gesamte Herde nach dem letzten Willen des Vaters zu teilen, und siehe da - der Älteste bekam neun der Tiere, der Mittlere sechs, der Jüngste zwei, das waren eben die Hälfte, ein Drittel und ein Neuntel, und auf dem Kamel, das übrig blieb, ritt der Weise - denn es war das seine - lächelnd davon.
In den Überlieferungen wechseln manchmal die Zahlen, z.B. funktioniert die Sache auch mit 11 Kamelen und den Anteilen 1/2 , 1/4 , 1/6 oder mit 23 Kamelen und den Anteilen 3/8 , 1/3 , 1/4 .
Es stellen sich zwei Fragen:
1.
Nach der Aufteilung des Erbes sind offenbar alle zufrieden. Aber ist die Aufteilung auch gerecht?
2.
Warum klappt der Trick des Pilgers eigentlich so gut? Man findet leicht ähnliche Beispiele, bei denen selbst nach der Zugabe von mehreren Kamelen eine ganzzahlige und vollständige Aufteilung des Erbes nicht möglich ist, etwa mit 27 Kamelen und den Anteilen 1/2 , 1/4 , 1/7 . Deshalb lautet die Verallgemeinerung des Problems:
Der Vater vererbt n Kamele auf m Erben, deren Erbanteile rational sind und in der Summe weniger als 1 ergeben. Der Pilger darf k Kamele hinzu geben und erhält sie nach der Erbaufteilung wieder zurück.
Wann geht unter diesen Umständen die Teilung des Erbes glatt auf?
Zu 1.
Aus der Erzählung geht hervor, dass vom Erbe nichts übrig bleiben soll, d.h. das Erbe muss vollständig auf die drei Söhne aufgeteilt werden. Durch die Anteile 1/2 , 1/3 , 1/9 ist aber nur über 17/18 des Erbes verfügt worden. Die gerechte Lösung ist wohl, die Verhältnisse der Erbanteile untereinander zu wahren (d.h. beispielsweise, dass der zweite Sohn dreimal so viel erhalten muss wie der dritte), indem man sie alle mit dem gleichen Faktor, nämlich 18/17 multipliziert: Man erhält 9/17 , 6/17 , 2/17 . Das ergibt in der Summe 1 und führt auf genau die gleiche Aufteilung wie die des Pilgers. Hätten die Brüder also einen weisen und mathematisch beschlagenen Richter befragt, hätten sie nicht der Hilfe des Pilgers bedurft.
Fazit: Die Aufteilung ist gerecht, und der Vater war nicht so dumm, wie mancher vielleicht denken mag.
Gilt das auch für andere Zahlenbeispiele?
In 2. wird eine Verallgemeinerung untersucht mit n Kamelen, m Erben und weiteren k Kamelen, die der Pilger hinzu gibt. Die Teilung nach dem Verfahren des Pilgers ist dann immer gerecht (falls sie funktioniert, d.h. wenn nur ganze Kamele verteilt werden und wenn für den Pilger genau seine k Kamele übrig bleiben): Die Erbanteile bezeichnen wir mit r 1 , r 2 , ... r m . Dann erhält der i-te Erbe r i · (n + k) Kamele. Da der Faktor n + k bei allen Erben gleich ist, werden die Verhältnisse der Erbanteile untereinander gewahrt. Die genaue Rechnung sieht so aus:
Gerechterweise zustehen würden dem i-ten Erben
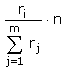
Kamele. Da der Pilger seine k Kamele zurückerhalten soll, muss außerdem gelten:
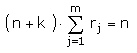
Daraus folgt aber
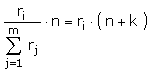
Also ist die Erbaufteilung gerecht.
Zu 2.
Das Verfahren des Pilgers ist genau dann erfolgreich, wenn gilt:
a) Nach der Erbaufteilung bleiben genau k Kamele übrig.
b) Die Erbaufteilung ist ganzzahlig.
Da die Erbanteile r i und die Zahl n vorgegeben sind, ist also nur ein passendes k zu suchen.
Mit den Bezeichnungen
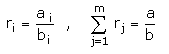
(a i , b i teilerfremd) muss dann wie in 1. gelten: a / b = n / (n + k) und r i · (n + k) ganzzahlig; letzteres bedeutet, dass alle b i Teiler von n + k sind. Somit ist (in mathematischer Formulierung) das Verfahren des Pilgers genau dann durchführbar, wenn es eine natürliche Zahl k gibt mit:

kgV ist dabei das kleinste gemeinsame Vielfache, also hier der Hauptnenner der Brüche. Da in a1) die Darstellung von a / b beliebig ist, lässt sich auch b = kgV { bi } wählen. Dann muss aber a ein Teiler von n sein, so dass wir zur folgenden Lösung kommen:
Man addiert alle Erbanteile zu einem Bruch unter Verwendung des Hauptnenners und prüft, ob der Zähler ein Teiler von n ist. Genau in diesem Falle ist eine Erbaufteilung nach dem Verfahren des Pilgers möglich.
Nach a1) ist dann k = n · ( b/a - 1 ) .
Falls das zu schnell ging, hier noch einmal der Nachweis der Äquivalenz:
Wenn a1), b1) gilt, dann ist b Teiler von n + k und somit a Teiler von n.
Umgekehrt: Wenn a ein Teiler von n ist, dann wählt man k = n · (b/a - 1) und erhält a1); b teilt dann n + k, also ist b1) erfüllt.
Pilger-Trick im engeren Sinne: k = 1
Natürlich lässt sich darüber streiten, ob der Pilger wirklich beliebig viele Kamele hinzu stellen darf. Wem das zu weit von der alten Erzählung weg führt, der mag sich fragen, welche Lösungen es für genau ein Pilger-Kamel gibt. Das lässt sich nun mit den Bezeichnungen von oben leicht angeben, es muss gelten: a / b = n / (n + 1) und b teilt n + 1 . Da sich aber n / (n + 1) nicht kürzen lässt, wird die Sache einfach:
a = n und b = n + 1 .
"Schöne" Lösungen
Als "schöne" Lösungen werden hier solche bezeichnet, die dem ursprünglichen Problem ganz ähnlich sind, also soll m = 3 und k = 1 gelten; außerdem sollen nur Stammbrüche (d.h. mit Zähler 1) für die Erbanteile vorkommen. Dann ist klar, dass nur endlich viele "schöne" Lösungen existieren, denn die Nenner dieser Stammbrüche können nicht beliebig groß werden. Genauer: Es muss gelten
1 / b 1 + 1 / b 2 + 1 / b 3 = n / (n + 1) oder 1 / b 1 + 1 / b 2 + 1 / b 3 + 1 / (n + 1) = 1
Für diese Gleichung findet man schnell genau 12 Lösungen. Unter diesen sind natürlich diejenigen aus der Problemstellung mit 17 und mit 11 Kamelen, aber es geht auch z.B. mit 41 Kamelen und den Anteilen 1/2 , 1/3 , 1/7 .
Aber sind diese wirklich alle "schön"? Offenbar möchte der Vater seine Söhne dem Alter nach in wachsender Höhe bedenken, so dass der Älteste die meisten und der mittlere Sohn die zweitmeisten Kamele erbt. Also sollten keine gleichen Erbanteile vorkommen, wie zum Beispiel in der Lösung mit 9 Kamelen und den Anteilen 1/2 , 1/5 , 1/5 . Dann bleiben nur noch 7 Lösungen übrig:
7 Kamele, Erbteilung 1/2 , 1/4 , 1/8
11 Kamele, Erbteilung 1/2 , 1/4 , 1/6 oder 1/2 , 1/3 , 1/12
17 Kamele, Erbteilung 1/2 , 1/3 , 1/9
19 Kamele, Erbteilung 1/2 , 1/4 , 1/5
23 Kamele, Erbteilung 1/2 , 1/3 , 1/8
41 Kamele, Erbteilung 1/2 , 1/3 , 1/7
Die Pilger-Gewinn-Variante und eine stochastische Lösung
Im Buch Beremis der Zahlenkünstler von Malba Tahan gibt es eine Variante unserer Erzählung, in der der Pilger einen Profit einheimst. Dort steht n = 35 statt n = 17, die Erbanteile sind wie oben. Da 17 kein Teiler von 35 ist, lässt sich das Problem eigentlich nicht lösen, aber im Buch lesen wir, dass der Pilger ein Kamel hinzugibt, den Brüdern ihre Erbschaft zuteilt, nämlich 18, 12 und 4 Kamele, und somit außer seinem eigenen noch ein weiteres Kamel übrig behält. Von diesem Kamel heißt es im Buch:
" ... das andere gehört billigerweise mir, weil ich Euer Problem mit der Erbschaft zur allgemeinen Zufriedenheit gelöst habe." - "Ihr seid wahrhaftig klug, o Fremder!" rief der älteste der Brüder aus. "Mit Eurer Einteilung sind wir vollauf zufrieden, und wir sind auch überzeugt, dass sie gerecht durchgeführt worden ist!" Der listige Beremis - ein Meister der Zahlen - suchte sich alsdann eines der schönsten Kamele der Herde aus ...
Was hätten die Brüder auch anders sagen können? Vielleicht hätte ein weiser Richter ihnen empfohlen, die Aufteilung von 34 Kamelen wie Beremis vorzunehmen und dann für das 35. Kamel 9 weiße Perlen für den Ältesten, 6 blaue Perlen für den Mittleren und 2 gelbe Perlen für den Jüngsten in einen Beutel zu füllen und damit den glücklichen Erben dieses letzten Kamels auszulosen.
Schlussbemerkung zu der alten Erzählung, wie sie in der Aufgabenstellung wiedergegeben wird:
Ist "störrische Zahl" für eine Primzahl nicht eine hübsche Umschreibung?
Kategorie: Zahlen und Zahlsysteme, Berechnung von π