Problem des Monats September 2001

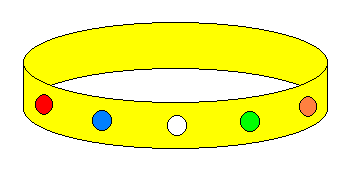
Ein Versandhaus macht eine Werbeaktion. Es bietet 25.000 Armreife mit eingelassenen farbigen Perlen zu einem Sonderpreis an. Jede Kundin soll in den Besitz eines Unikats kommen: Obwohl bei jedem Armreif die gleichen Perlenfarben verwendet werden, ist die Anordung (Reihenfolge) der Farben bei jedem Reif garantiert einzigartig.



Ansonsten sind alle Armreife in jeder Hinsicht symmetrisch und von gleicher Machart - insbesondere kommen bei allen genau die gleichen Perlenfarben vor. Keine Perlenfarbe kommt auf einem Reif mehr als einmal vor.

Wie viele Perlen muss ein solcher Armreif mindestens haben?

Lösung

Das Versandhaus muss Armreife mit mindestens 10 Perlen herstellen.

Es ist hier nach der Anzahl von Permutationen gefragt, d.h. es soll die Anzahl aller möglichen Reihenfolgen von angeordneten Objekten (Perlen) bestimmt werden.

Wenn  n  verschiedene Perlen in einer Reihe liegen, ist diese Anzahl leicht anzugeben:

Es gibt  n ! = 1 · 2 · ... · n  mögliche Reihenfolgen. Das macht man sich klar durch die (induktive) Überlegung, dass ein neu hinzugenommenes ( n + 1 )-tes Objekt in jeder der  n !  Anordnungen  n + 1  Plätze finden kann (zwischen den  n  schon vorhandenen oder am Rand); somit haben wir nun  n ! · ( n + 1 ) = ( n + 1 ) !  mögliche Reihenfolgen, was die angegebene Formel für alle natürlichen Zahlen  n  beweist.



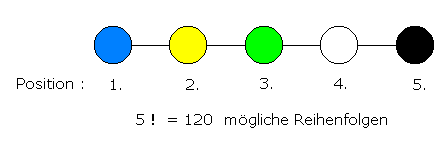
Nun liegen aber die Perlen nicht in einer Reihe, sondern auf einem Reif, also im Kreis angeordnet. Es gibt also keinen ersten, zweiten ... oder letzten Platz, da sich der Reif beliebig drehen lässt. Wenn man sich nun vorstellt, dass die Perlen eine nach der anderen platziert werden, so spielt es keine Rolle, wo die erste Perle eingesetzt wird; erst die relativen Positionen der anderen  n - 1  Perlen zur ersten führen zu unterscheidbaren Reihenfolgen auf dem Reif. So könnte man etwa die weiße Perle immer zuerst einsetzen und dann die übrigen Positionen im Uhrzeigersinn von  1  bis  n - 1  durchnummerieren:

Man erhält dann  ( n - 1 ) !  mögliche Reihenfolgen der Perlen.

Dieses Problem ist an einer Reihe junger Mathematikerinnen und Mathematiker "ausprobiert" worden. Nicht wenige haben an dieser Stelle aufgehört und  ( n - 1 ) !  für die Lösung verwendet; vielleicht deshalb, weil sie schon gelernt hatten, dass man  n  Leute auf  ( n - 1 ) !  verschiedene Weisen um einen runden Tisch setzen kann (wobei "Drehungen" des Tischs mitsamt den Stühlen keine Rolle spielen sollen; zwei Sitzordnungen gelten als gleich, wenn jeder Gast den gleichen Nachbarn zur Linken hat). Aber das Problem mit den Armreifen ist damit nicht richtig gelöst.

Wegen der Symmetrie der Armreife ist kein "unterer" oder "oberer" Rand vorgegeben, d.h. man kann einen Reif auf zwei Weisen auf den Tisch legen. Für die Perlen bedeutet das lediglich die Vertauschung von Uhrzeigersinn und Gegenuhrzeigersinn (falls es mehr als zwei sind). Es lassen sich also zwei Armreife nur dann als wirklich verschieden auffassen, wenn sie sich nicht zur Deckung bringen lassen, egal wie man sie hält. Diese beiden Reife wären somit keine Unikate:



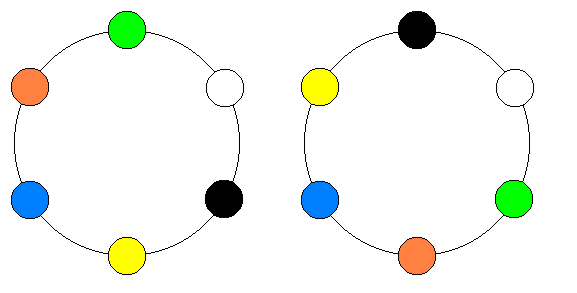
In den  ( n - 1 ) !  Reihenfolgen für die Anordnung der  n  Perlen im Kreis gelten aber diese beiden Bilder als verschieden, und so ist es bei allen Anordnungen von mehr als zwei Perlen, die man durch "Herumdrehen" (Kippen) ineinander überführen kann.

Also kommen für  n > 2  nur noch  ( n - 1 ) ! / 2  Anordnungen der Perlen in Frage. Diese Zahl soll nun mindestens 25.000 betragen:

( n - 1 ) ! / 2  >  24.999     also:     n > 9

Wenn das Versandhaus also Armreife mit 10 verschiedenfarbigen Perlen herstellt, können die Käuferinnen aller 25.000 Armreife ein Unikat erhalten.