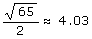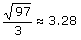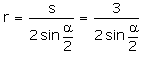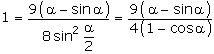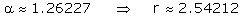Problem des Monats November 2000
Die Lösung steht im unteren Teil der Seite.
Im vorigen Monat haben Sie sich (hoffentlich) mit der mathematischen Problematik von Wiesen vertraut gemacht. Sie brauchen sich nicht umzustellen: Hier kommt die nächste Wiesenaufgabe.
Die Brüder Jakob B. und Johann B. bewirtschaften gemeinsam eine Anzahl von Wiesen, die sie in der Nähe von Basel geerbt haben. Sie streiten sich viel (meist darüber, wer der bessere Mathematiker ist) und beschließen daher eines Tages, die Wiesen aufzuteilen. Diese sind sehr unterschiedlich gelegen, deshalb soll von jeder Wiese genau die Hälfte an jeden Bruder fallen. Jakob und Johann stellen fest, dass sie alle notwendigen Halbierungen durchführen können, indem sie jeweils eine gerade Grenze von Rand zu Rand ziehen. Auf diesen neuen Grenzen sollen Zäune gezogen werden, die natürlich möglichst kurz sein sollen. Die beiden Brüder geraten ins Nachdenken. Jakob fordert seinen Bruder mit einer Aufgabe heraus:
Ist die kürzeste Grenze immer gerade?
Johann kann das beantworten! Sie auch?
Johann nimmt Revanche und fragt seinen Bruder:
Kann es auch Wiesen geben, die sich durch keine gerade Strecke gerecht teilen lassen?
Mit Genugtuung präsentiert Jakob kurz darauf die Antwort. Wie lautet sie?
Bevor Sie anfangen, über die beiden Probleme nachzudenken, soll die Aufgabenstellung präziser formuliert werden. Unter einer Wiese soll eine ebene, endliche Fläche verstanden werden, die von einem geschlossenen Polygonzug (n-Eck) ohne Doppelpunkte (Berühr- oder Kreuzungspunkte) begrenzt wird. (Also bitte keine sphärische Geometrie wie im Oktober; hier ist nur ebene Geometrie verlangt.)
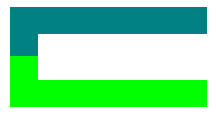
So könnten die Wiesen aussehen:

So dürfen die Wiesen nicht aussehen:

Die Teilungslinie soll in einem Stück von Rand zu Rand verlaufen und zwei gleich große zusammenhängende Wiesenstücke erzeugen, z.B. so:
Aber nicht so:

Wenn nun (im ersten Problem) gefragt wird, ob die kürzeste Teilungslinie immer gerade ist, so wird natürlich vorausgesetzt, dass die Wiese überhaupt (mindestens) eine gerade Strecke zur Teilung zulässt (so wie bei den Brüdern B.). Beim zweiten Problem ist dann von irgendwelchen anderen Wiesen die Rede, nicht von denen der Brüder B.
Lösung
Hoffentlich hat niemand versucht zu beweisen, dass die kürzeste Teilungslinie gerade ist (falls es überhaupt eine gerade Teilung gibt) oder dass es immer eine gerade Teilungsstrecke gibt. Allgemeine Sätze dieser Art sind bei der Vielfalt der erlaubten Polygone wohl eher schwer zu beweisen. Wer also darauf vertraut hat, dass die Lösung nicht so schwierig sein kann, ist gleich auf die Suche nach Gegenbeispielen gegangen. Mit ein wenig Probieren kann man eine Wiese finden, die zwar eine gerade Teilung erlaubt, aber deren kürzeste Teilung nicht gerade ist, und eine andere Wiese, die überhaupt keine gerade Teilung zulässt.
Wir fangen mit dem zweiten Problem an. Hier ist eine Wiese, die sich offenbar nicht durch eine gerade Grenze von Rand zu Rand in zwei gleich große Wiesen teilen lässt:

Falls Sie eine wesentlich einfacher geformte Wiese mit der gleichen Eigenschaft kennen, lassen Sie es mich wissen.
Das erste Problem ist auch nicht schwer, führt aber zu einer weiteren interessanten Fragestellung und bekommt daher etwas mehr Raum. Zunächst kann man, ebenfalls durch Probieren, ein Gegenbeispiel finden:

Die kürzeste gerade Teilung geht so:
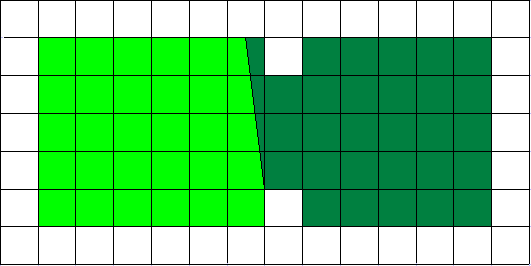
Die Grenze hat dann die Länge
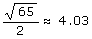
Die folgende Grenzziehung ist kürzer:

Das Dreieck muss den Flächeninhalt 1 haben; dann hat der Zaun die Länge
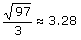
Damit ist ein Gegenbeispiel gefunden und das Problem gelöst. Aber man
möchte nun natürlich gerne noch wissen, welches die kürzeste Grenze
überhaupt ist.
Diese Frage führt uns in das Gebiet der Variationsrechnung. Dort untersucht man u.a. Problemstellungen der folgenden Art: Welche Kurve (aus einer vorgegebenen Menge von Kurven) hat eine bestimmte Extremaleigenschaft? Ein berühmtes Beispiel ist das isoperimetrische Problem: Welche geschlossene ebene Kurve von vorgegebener Länge umschließt die größte Fläche? Antwort: Der Kreis. Das "duale" Problem dazu lautet: Welche geschlossene ebene Kurve, die einen vorgegebenen Flächeninhalt umschließt, hat die kleinste Länge? Gleiche Antwort: Der Kreis. Nun ist unsere Frage nach der kürzesten Grenze zur Halbierung der Wiesenfläche ja ganz ähnlich.
Welche Kurve zwischen zwei Punkten, die zusammen mit der Strecke zwischen diesen Punkten den Flächeninhalt 1 umschließt, ist die kürzeste?
Das dazu duale Problem (mit derselben Lösung) lautet: Welche Kurve fester Länge zwischen zwei Punkten umschließt zusammen mit der Strecke zwischen diesen Punkten den größten Flächeninhalt?
Dieses Problem hat einen Namen: Es ist das Problem der Dido. Dido war die sagenhafte Königstochter aus der phönizischen Stadt Tyros am Mittelmeer (heute Sur im Libanon), die als Gründerin Karthagos gilt. Dort im Norden Afrikas war Dido nach einer Flucht übers Meer gelandet, nachdem ihr Bruder Pygmalion ihren Gemahl ermordet hatte. Sie gewann mit einer List ein bedeutendes Landgebiet: Sie erbat sich so viel Siedlungsfläche, wie mit einer Stierhaut zu umfassen sei. Dies wurde ihr ahnungslos gewährt. Dido schnitt die Haut in feine Streifen, verknotete diese und legte damit eine lange Kurve ins Land, deren Endpunkte an der Küste lagen.
Es ist nicht überliefert, ob Dido die bestmögliche Kurve gewählt hat. Erst nach der Begründung der Infinitesimalrechnung im 17. Jh. wurde ihr Problem systematisch behandelt. Die Lösung lautet, dass die Kurve ein Stück eines Kreises sein muss. Also sieht die optimale Grenzziehung so aus:
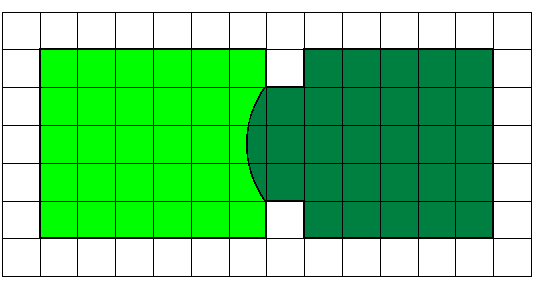
Wie lang ist diese Grenze?
Für den Flächeninhalt A des Kreisabschnitts gilt

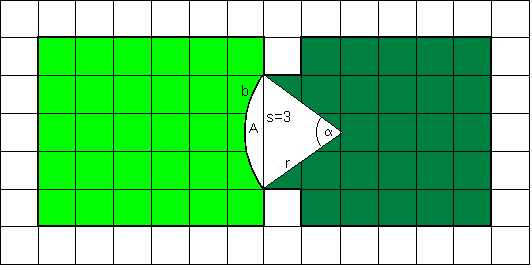
Nun ist hier A = 1 und
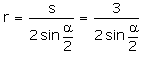
Man erhält so die Gleichung
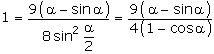
mit der Näherungslösung
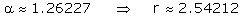
Damit kann man den Kreisbogen zeichnen. Seine Länge b (und damit die Lösung des Minimierungsproblems) berechnet man zu
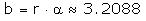
Stand 2003-01-16
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite