Es genügt, für einen Breitenkreis der konstanten Höhe h (wie in der Tabelle auf der Hauptseite) den Beweis zu führen, denn jeder Kreis auf der Kugel lässt sich in diese Position drehen. Im Beweis darf auch h < 0 sein.
Die Koordinaten xs und ys liest man in (7) auf der Hauptseite ab, und aus der Tabelle die xs-Koordinate des Mittelpunkts m = cos φ/(sin φ + sin h). Es ist nun zu zeigen, dass (xs - m)2 + ys2 das Quadrat des in der Tabelle angegebenen Radius cos h /(sin φ + sin h) ist. Bei der Rechnung kann man sich ein wenig durch ein Mathematik-Programm helfen lassen; die folgenden Rechenschritte sind mit MATHEMATICA® durchgeführt und ausgegeben worden. Im ersten Schritt werden lediglich alle Terme auf den Hauptnenner gebracht und die Quadrat-Klammern im Zähler aufgelöst. Im zweiten Schritt wird im Zähler cos2h ausgeklammert. Mit cos2x + sin2x = 1 wird der Zähler vereinfacht. Der letzte Schritt ist nur noch eine Kürzung.
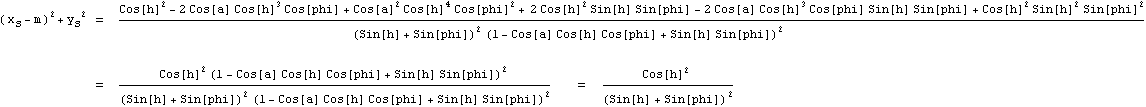
Die stereographische Projektion findet man z.B. im Lehrbuch Kugelgeometrie von H.-G. Bigalke sehr gut dargestellt; den Satz über die Kugelkreise (mit einem anderen Beweis) findet man dort unter 5.5.
zurück zur Briefmarkenseite # 69
zur Leitseite